离散数学(2) 期末真题

2025春 离散数学(2) 周旻 期末考试回忆版

一、选择题 (4pts)

1. (2pts) 以下关于群的说法中，正确的是：
   A. 存在无限群，其只有有限个子群
   B. 存在群 $G$ 是其两个真子群的并
   C. 所有元素的阶都是有限的群必为有限群
   D. 存在无限群，其有且仅有两个有限阶元素

2. (2pts) 以下关于置换的说法中，错误的是：
   A. 轮换 $(i_1 i_2 \cdots i_k)$ 是偶置换当且仅当 $k$ 是偶数
   B. 置换 $\sigma$ 是偶置换当且仅当 $\tau^{-1}\sigma\tau$ 是偶置换
   C. 轮换 $(i_1 i_2 \cdots i_k)$ 可表示为 $(i_1 i_2)(i_2 i_3)\cdots(i_{k-1} i_k)$
   D. 任意两个偶置换的乘积仍然是偶置换

二、填空题 (16pts)

3. (2pts) 对称群 $S_8$ 中，不相交轮换乘积表示形式为 $(abc)(def)(gh)$ 的元素共有 ____ 个。

4. (2pts) 将置换 $\begin{pmatrix} 1&2&3&4\\4&3&1&2\end{pmatrix}\circ\begin{pmatrix} 1&2&3&4\\3&1&4&2\end{pmatrix}$ 表示成不相交轮换的乘积形式：________。

5. (2pts) 已知一棵树中，有 $1$ 个 $5$ 度顶点，$2$ 个 $4$ 度顶点，$3$ 个 $3$ 度顶点，若干个 $2$ 度顶点，则这棵树有 ____ 个叶子节点。

6. (2pts) 点数为 $8$ 的平面自对偶图的边数为 ____。

7. (4pts) 完全二分图 $K_{r,s}(r\geq s)$ 中，两两不相关的边最多有 ____ 条（两条边相关当且仅当它们有公共顶点）；该二分图是哈密顿图的充要条件是 ________。

8. (4pts) 下图 ____ （是/不是）平面图，简述原因：____________。

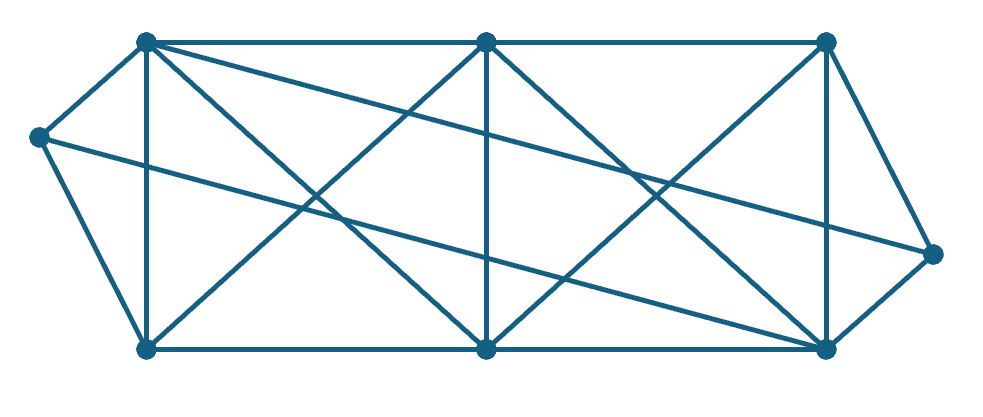
三、建模题 (32pts)

9. (8pts) 如下图所示，$A$ 从顶点 $v_2$ 出发，$B$ 从顶点 $v_1$ 出发，要求两人遍历完所有边至少一次后到达终点 $v_3$，谁到达更快谁就胜利。假设两人经过同一条边的时间相同，请问谁有必胜策略？

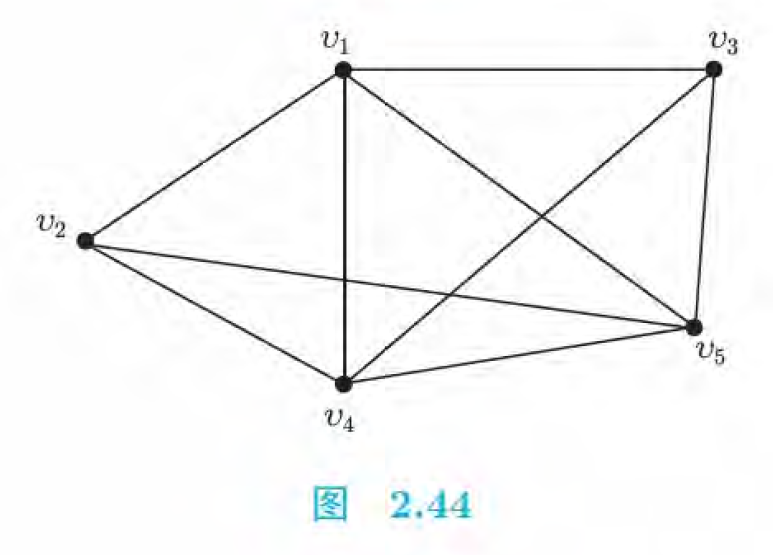
10. (8pts) 有 $5$ 个字符串 $bc,ed,ac,bd,abc$，能够用其中的一个字母代表该字符串并且不产生混淆？

11. (8pts) 有 $6$ 种货物各 $3$ 件，现有 $3$ 辆卡车，分别能装 $5,6,7$ 件货物，但每辆卡车每种货物最多装一件，能否将所有货物装上卡车？

12. (8pts) 利用 $PT$ 图求解下列关键路径问题，并给出每项工序的最晚启动时间。

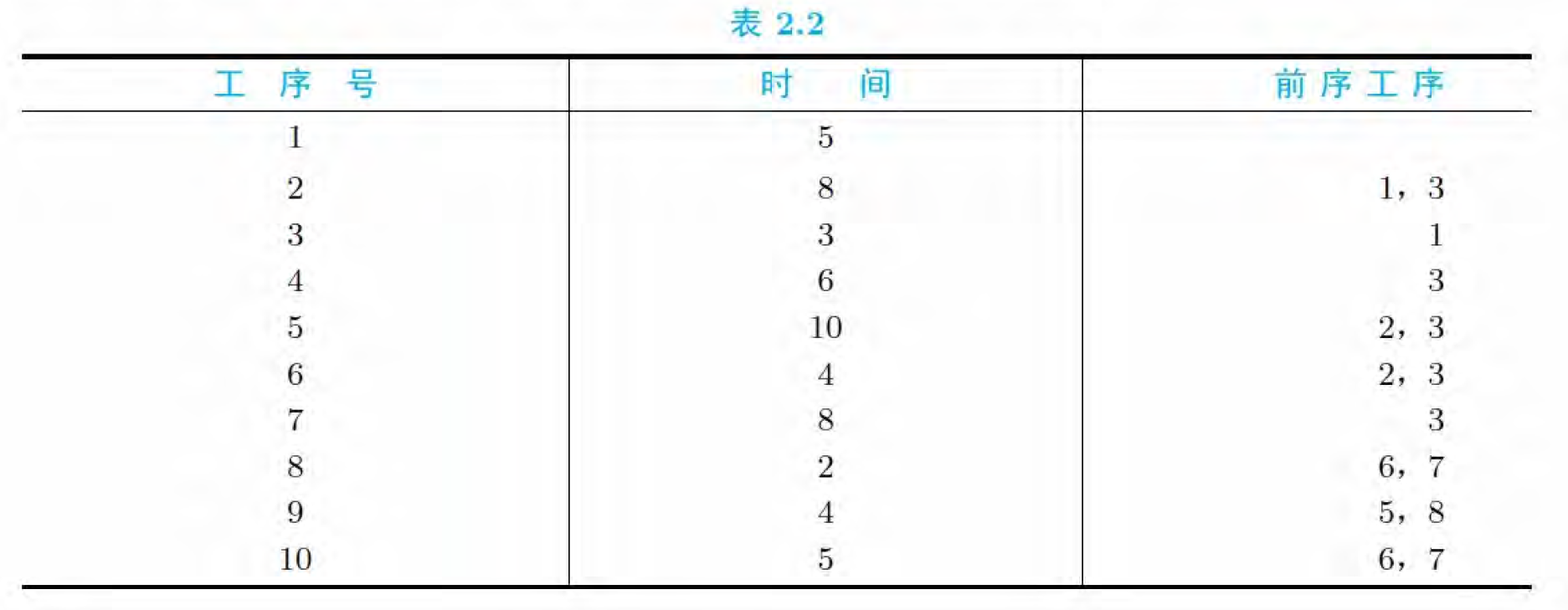
四、证明题 (38pts)

13. (4pts) 证明：下图中没有包含奇数条边的回路。

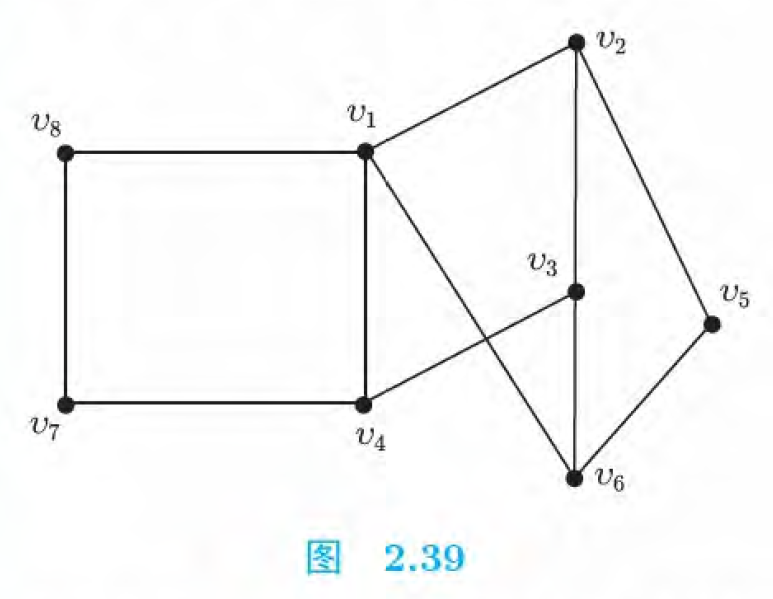
14. (6pts) 证明：若平面图中不存在边数 $\le 5$ 的回路，则至少有一个点的度数不超过 $2$。

15. (6pts) $n$ 个人中，设任意两人合在一起能认识其余 $n-2$ 个人，证明：他们可以站成一圈，使相邻者认识。

16. (6pts) 给出边权为正的无向连通图 $G=(V,E)$，并定义两点间的距离 $d(v_i,v_j)$ 为两点间最长的初级道路的长度。设 $G$ 中距离最大的两个点为 $s,t$，证明：对于任意 $v\in V$，有 $\displaystyle 2\cdot \max_{u\in V} d(u,v)\ge d(s,t)$。

17. (6pts) 定义映射 $T:A\to B$，其中 $(B,\times)$ 是群，定义映射乘法 $T_1\circ T_2(x)=T_1(x)\times T_2(x)$，证明：所有从 $A$ 到 $B$ 的映射关于 $\circ$ 构成群。

18. (6pts) 证明：对称群 $S_3$ 是最小的非交换群。（提示：证明阶数不大于 $5$ 的群都是交换群）

19. (4pts) 证明：有限 $\mathrm{Abel}$ 群 $G$ 中，$\displaystyle \prod_{g\in G} g=\prod_{a\in G,a^2=e} a$，其中 $e$ 是 $G$ 的幺元。

五、算法题 (10pts)

对于一个正权无向简单连通图，定义两点间某条路径的强度为路径上所有边权的最小值，定义两点间的距离为两点间所有路径强度的最大值。

如两点间的某条路径由 $3$ 条边组成，边权分别为 $2,3,5$，则该路径的强度为 $2$；若该两点间只有两条路径，且另外一条路径的强度是 $4$，则该两点间的距离为 $\max(2,4)=4$。

请设计一个算法，求出该图的一个支撑子图，使其满足以下要求：（1）该支撑子图连通；（2）该支撑子图中两点间的最小距离最大；（3）在满足（1）（2）的条件下，总边数最少。

20. (3pts) 证明：满足上述三个要求的支撑子图一定是原图的一棵支撑树。

21. (5pts) 以下伪代码是该问题的一个可行解，采用了类似 $\mathrm{Kruskal}$ 的思想，请阅读并完成填空：

int find(int n){
    while(n != parent[n]) {
        ____________(21.1)
    }
    return n;
}
void union(int x,int y){
    parent[x]=parent[y];
}
int main(){
    for(int i=1;i<=edges.num;i++)
        for(int j=i+1;j<=edges.num;j++)
            if(____________(21.2))
                swap(edges[i], edges[j]);
    blocks_cnt=n;
    for(int i=1;i<=edges.num;i++){
        int x=find(edges[i].start);
        int y=find(edges[i].end);
        if(x != y) {
            ____________(21.3)
            blocks_cnt--;     
        }
        if(__________(21.4)){
            print("%d",__________(21.5));
            return 0;
        }
    }
}

22. (2pts) 简要证明上述算法的正确性。