肆叁小灶第七讲 从 Huffman 树到信息论
肆叁小灶第七讲,介绍了信息论、编码理论和 $\mathrm{Huffman}$ 编码。
笃实 43 班的同学们大家好。本学期《肆叁小灶》将预计更新 3-4 期:本期我们将从《数据结构》课中介绍的 $\mathrm{Huffman}$ 树出发,讲解其背后的理论基础——编码理论与信息论;之后,我们将用 2-3 期的篇幅带大家从零开始了解人工智能技术,直至学术前沿。希望同学们能通过本学期的《肆叁小灶》系列推送,对人工智能有一个初步的认识,为下学期的《人工智能基础》课程做好准备。
废话不多说,让我们直接进入正题。
一、$\mathrm{Huffman}$ 编码
在《数据结构》课上,提到了 $\mathrm{Huffman}$ 树是“最优编码树”,但并没有给出具体的证明过程。事实上,由 $\mathrm{Huffman}$ 树构造而来的 $\mathrm{Huffman}$ 编码不仅是前缀码中最优的,也是所有唯一可译码中最优的;而在实际应用中,非唯一可译码并没有什么意义(因为它可能导致歧义),因此 $\mathrm{Huffman}$ 编码可以说是所有编码中最优的。
“唯一可译码”和“前缀码”并不等价。例如将符号集 ${A, B, C, D}$ 编码为 ${10, 00, 11, 110}$,这个编码并不是前缀码(因为 $11$ 是 $110$ 的前缀),但它是唯一可译的。为了区分 $C$ 和 $D$,我们只需要等待下一个 $1$ 出现:如果中间的 $0$ 的数量是偶数,我们解码 $11$,否则我们解码 $110$。
也正因此,$\mathrm{Huffman}$ 编码在数据压缩领域有着极其广泛的应用。下面,就让我们一步步来证明 $\mathrm{Huffman}$ 编码的最优性。
1.1 最优前缀码
首先,如果将 $01$ 编码视为一个二叉树,那么在前缀码所对应的二叉树中,码字一定对应于这棵树的叶节点。
这是因为,如果存在码字的对应节点不是叶节点,那么一定存在另一个码字的对应节点是这个节点的后代,也即这两个码字的对应节点在同一条路径上——这意味着前者是后者的前缀,而这与前缀码的定义相矛盾。
所以,给定一组符号及其频率,如果我们将每个符号与其频率视作一个带权的节点,那么最小化平均码长的问题就转化为:构造一个以上面这些带权节点为叶节点的二叉树,使得所有叶节点的加权路径长度之和最小。
接下来,我们可以注意到两个最优前缀码所必须的性质:
- 根据排序不等式,概率更大的符号应该具有更小的码长,即概率的排序应与码长的排序恰好相反;
- 其对应的二叉树不可能存在只有一个子节点的中间节点,否则可以将其子节点直接提升为其父节点的子节点,从而降低总权值。
上面的两个性质就可以导出一个结论:存在一个最优的前缀码,使得两个最不可能的码字仅在最后一位不同,即两个最不可能的码字是兄弟。这是因为:
- 这两个码字必须拥有同样且最大的码长(如果不是最大,则与上面的第一个性质矛盾;如果不相同,则只有一个码字拥有最大的码长,这说明这个码字在树上的父节点只有一个子节点,而这与上面的第二个性质矛盾);
- 如果它们没有相同的父节点,这意味着一定存在第三个拥有相同码长的码字(因为不存在只有一个子节点的中间节点),故可以将这两个码字与第三个码字交换,从而使得它们成为兄弟。
这也就是说,让这两个最不可能的码字成为兄弟不影响整体的最优性,那我们就不妨让它们成为兄弟。这样一来,我们就可以将它们合并为一个新的符号,其频率为这两个码字的频率之和:这是因为,只要获得了这个新符号的最优前缀码,我们只需要通过在其码字后分别添加 $0$ 和 $1$,就可以获得原来两个码字的最优前缀码。如此,我们就把问题的规模从 $n$ 降低到了 $n-1$。然后,我们就可以通过反复的合并操作,最终将问题简化为只有两个符号的情况,而这时显然只存在唯一且最优的前缀码:$0$ 和 $1$。
1.2 前缀码与唯一可译码
前面提到,唯一可译码和前缀码并不等价。但显然,前缀码一定是唯一可译的,而且是“即时可译”的:也就是说,在接收到一个码字流时,我们可以从左到右逐位读取码字,并且一旦读到一个完整的码字,就可以立即将其译码,而不需要等待后续的码字。而非前缀的唯一可译码则可能不具备这个性质,就比如前面提到的例子。
那么自然会有一个问题:是否有可能存在非前缀的唯一可译码,其平均码长小于所有前缀码的平均码长?如果能够证明其不存在,那么 $\mathrm{Huffman}$ 编码的最优性就可以推广到所有唯一可译码。事实上,这就是信息论中著名的 $\mathrm{McMillan}$ 定理。
首先,容易证明:存在一个码字长度为 $l_1,l_2,\cdots,l_n$ 的前缀码当且仅当 $\displaystyle \sum_{i=1}^n 2^{-l_i}\leq 1$。这是因为,如果给深度为 $l$ 的叶节点分配权值 $2^{-l}$,那么一个真二叉树中所有叶节点的权值之和为 $1$;而前缀码一定对应于一棵二叉树的叶节点,也即一个真二叉树叶节点的子集。我们称这个不等式为 $\mathrm{Kraft}$ 不等式。
接下来,如果我们能够证明所有唯一可译码都满足 $\mathrm{Kraft}$ 不等式,那么就说明对于任意唯一可译码,我们都可以找到一个前缀码,其码字长度与该唯一可译码相同,而这也就意味着该前缀码的平均码长与该唯一可译码相同。
假设某个随机消息有 $r$ 个可能的值 $u\in U$(这里集合 $U$ 表示消息字母表)。我们为这个随机消息设计一个唯一可译码,它为每个可能的符号 $u\in U$ 分配一个长度为 $l(u)$ 的码字,设 $l(u)$ 的最大值为 $l_{\max}$。接下来我们考虑 $\displaystyle\left(\sum_{u\in U}2^{-l(u)}\right)^v$,其中 $v$ 为正整数。容易发现,这等价于 $\displaystyle \sum_{u_1\in U}\sum_{u_2\in U}\cdots\sum_{u_v\in U}2^{-(l(u_1)+l(u_2)+\cdots+l(u_v))}=\sum_{w\in U^v}2^{-l(w)}$,其中 $w$ 表示长度为 $v$ 的消息序列,$l(w)$ 表示该消息序列的码字长度。
接着,我们把 $U^v$ 中所有码字长度相同的消息序列合在一起。显然长度为 $v$ 的消息序列的码字长度不可能超过 $vl_{\max}$,因此我们可以把上面的求和写成 $\displaystyle \sum_{t=1}^{vl_{\max}}w(t)2^{-t}$,其中 $w(t)$ 表示码字长度为 $t$ 的消息序列的数量。又由于我们使用的是唯一可译码,所以消息序列必然也是唯一可译的,这要求码字长度为 $t$ 的消息序列的数量不能超过 $2^t$,否则就会出现码字冲突。因此,我们有 $w(t)\leq 2^t$,从而 $\displaystyle \sum_{t=1}^{vl_{\max}}w(t)2^{-t}\leq \sum_{t=1}^{vl_{\max}}2^t2^{-t}=vl_{\max}$,也即 $\sum_{u\in U}2^{-l(u)}\leq (vl_{\max})^{\frac{1}{v}}$。
由于上式对任意正整数 $v$ 都成立,我们令 $v\to +\infty$,就得到 $\displaystyle \sum_{u\in U}2^{-l(u)}\leq 1$,而这正是 $\mathrm{Kraft}$ 不等式。这样,我们就完成了 $\mathrm{McMillan}$ 定理的证明,从而证明了 $\mathrm{Huffman}$ 编码在所有唯一可译码中的最优性。
二、平均码长的理论下界
想必大家都听说过这样一个轶闻:苏联曾试图研究三进制计算机,因为理论上最高效的进制是 $e$ 进制,但现实中进制只能取整数,因此二进制和三进制就成了妥协。
那么类似地,在编码领域,$\mathrm{Huffman}$ 编码是否也只是“码长只能取整数”的一种妥协?如果我们允许码长取非整数值,是否能够获得更优的编码?如果是,这种非整数码长编码的平均码长是可以任意小,还是存在某个理论下界?而这就是信息论中的另一个重要结论:大名鼎鼎的信息熵。
2.1 信息量的度量
首先:什么是信息?让我们看一个例子:
你观察一个赌徒抛一个公平的硬币,然后告诉你的朋友。通过这样做,你给了你的朋友一定量的信息。接着,你继续观察他掷一个公平的骰子,然后告诉你的朋友。通过这样做,你又给了你的朋友一定量的信息。
现在的问题是:这两次你给朋友的信息量一样多吗?
显然,后者包含的信息量要大于前者。这是因为,前者只可能有两种回答:正或反,而后者则有 $6$ 种可能。从中我们可以看出,信息量的大小应该与可能的答案数量 $r$ 正相关。
让我们继续上面的例子:接下来,你观察赌徒掷骰子三次。同样,你记录下三次的结果并告诉你的朋友。
显然,这次你给朋友的信息量是前一次的三倍。从中我们可以看出,“信息”在某种程度上应该是可加的。
但现在我们面临一个新问题:以上面赌徒的例子为例,后者可能的答案数量是前者的 $36$ 倍,但我们希望信息量只是三倍的关系。于是,我们自然会想到,信息量应该与可能的答案数量的对数成正比。
但如果每个答案发生的概率并不相同呢?显然,如果一个事件几乎必然发生,那么它发生时所包含的信息量就应该很小;反之,如果一个事件几乎不可能发生,那么它发生时所包含的信息量就应该很大。
定量地说,假设有一枚神秘的四面体骰子,其中某一面朝下的概率为 $\frac{1}{2}$,其余三面朝下的概率均为 $\frac{1}{6}$。那么,当你告诉朋友 $\frac{1}{2}$ 面朝下时,所包含的信息量其实就相当于一个公平硬币的投掷结果。
可见,我们可以通过对概率取倒数把非等可能事件转化为等可能事件;接着,根据上面的分析,我们就可以对其取对数,从而得到信息量的度量。也就是说,信息量应该与概率的负对数成正比。
形式化地,我们考虑一个随机变量 $X$,它有 $n$ 个可能的取值 $x_1,x_2,\cdots,x_n$,对应的概率分别为 $p(x_1),p(x_2),\cdots,p(x_n)$。那么,当 $x_i$ 发生时,所包含的信息量可以定义为:$I(x_i)=\log\left(\frac{1}{p(x_i)}\right)$。接着,再对所有可能的取值求期望,我们就得到了这个随机变量的信息量的度量:$\displaystyle H(X)=\mathbb E[I(X)]=\sum_{i=1}^n p(x_i)I(x_i)=-\sum_{i=1}^n p(x_i)\log p(x_i)$,这就被称为信息熵。
对数的底数可以取任意值(不同的底数等价于一个常数因子),在信息论中通常取 $2$,因为这样我们就可以直接使用比特来作为信息熵的单位了。
2.2 信源编码定理
有了信息熵的概念,平均码长存在理论下界就是显而易见的了:
我们将原始符号集 $U$ 中的每个符号 $u$ 视作一个随机变量 $X$ 的取值,其概率为 $p(u)$。那么,一单位的 $X$ 所包含的信息量就是 $H(X)$;而一单位的 $01$ 码最多只能携带 $1$ 比特的信息量(当且仅当 $01$ 等概率时,这可以通过简单的计算来验证),因此要传输 $H(X)$ 比特的信息量,至少需要 $H(X)$ 单位的码字长度。
这就是著名的 $\mathrm{Shannon}$ 第一定理,又称信源编码定理。它告诉我们,任何编码的平均码长都不能小于信息熵 $H(X)$,取等的一个必要条件是 $01$ 码等概率出现。
三、通信误差
然而,在现实中,由于信道噪声的存在,传输过程中往往会出现误码现象。形式化地,假设信源给出的是随机变量 $X$,接收端接收到的是随机变量 $Y$,则转移概率矩阵 $P_{Y|X}(y_j|x_i)$ 并不一定是单位矩阵。
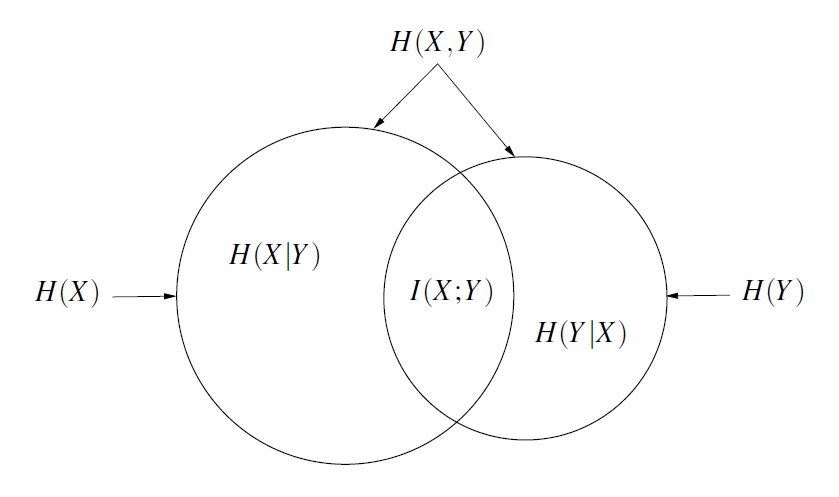
3.1 条件熵、联合熵与互信息
在概率论课程中,我们学习过条件分布和条件期望的概念。类似地,在信息论中,我们也可以定义条件熵:$\displaystyle H(Y|X=x_i)=-\sum_j P_{Y|X}(y_j|x_i)\log P_{Y|X}(y_j|x_i)$ 表示在已知 $X=x_i$ 的条件下,$Y$ 的不确定性;再对所有可能的 $x_i$ 求期望,我们就得到了条件熵:$\displaystyle H(Y|X)=\sum_i P_X(x_i)H(Y|X=x_i)=-\sum_{i}\sum_{j}P_{X,Y}(x_i,y_j)\log P_{Y|X}(y_j|x_i)$。
条件熵衡量了信道引入的不确定性。不难发现:在无损信道中转移概率矩阵 $P_{Y|X}(y_j|x_i)$ 是单位矩阵,条件熵 $H(Y|X)=0$;而在完全噪声信道中(即接收到的信号与发送的信号独立),$P_{Y|X}(y_j|x_i)=P_Y(y_j)$,条件熵 $H(Y|X)=H(Y)$。
将信源本身的不确定性和信道引入的不确定性相加,我们就得到了联合熵:$\displaystyle H(X,Y)=H(X)+H(Y|X)=-\sum_{i}\sum_{j}P_{X,Y}(x_i,y_j)\log P_{X,Y}(x_i,y_j)$。联合熵衡量了信源和信道整个系统的总不确定性。
我们还可以定义互信息:$\displaystyle I(X;Y)=H(X)-H(X|Y)=\sum_{i}\sum_{j}P_{X,Y}(x_i,y_j)\log\left(\frac{P_{X,Y}(x_i,y_j)}{P_X(x_i)P_Y(y_j)}\right)$。互信息衡量了接收到 $Y$ 后对 $X$ 的不确定性减少了多少。
互信息有两个极端情况:当信道无损时,接收到 $Y$ 后 $X$ 的不确定性完全消失,因此 $I(X;Y)=H(X)$;而当 $X$ 和 $Y$ 独立时,接收到 $Y$ 后对 $X$ 的不确定性没有任何减少,因此 $I(X;Y)=0$。
下面这张图可以帮助大家理解这些概念之间的关系:
3.2 信道容量与信道编码定理
互信息 $I(X;Y)$ 依赖于输入分布 $P_X(\cdot)$。如果我们能够选择输入分布,那么我们就可以通过选择不同的输入分布来最大化互信息,从而最大化每次传输所能携带的信息量。这个最大值就被称为信道容量:$\displaystyle C=\max_{P_X(\cdot)}I(X;Y)$。
一个输入分布 $P_X(\cdot)$ 能够达到信道容量 $C$ 需要满足的条件称为 $\mathrm{Karush–Kuhn–Tucker(KKT)}$ 条件, 其形式为:$I(x;Y)=C$ 当且仅当 $P_X(x)>0$;$I(x;Y)\le C$ 当且仅当 $P_X(x)=0$。这个条件其实非常直观:如果某个输入符号 $x$ 的平均互信息小于信道容量 $C$,那么我们就不应该使用它(即 $P_X(x)=0$),否则就无法达到信道容量。
在通信中,往往需要经过两道编码过程:信源编码和信道编码。直观地说,信源编码是用于将原始符号集以尽可能高的效率压缩到 $01$ 码中,而信道编码则是用于将 $01$ 码以尽可能高的可靠性传输到接收端,而这必然要求在传输过程中引入冗余。
信道传输速度就是用于衡量信道编码引入的冗余量的,其定义为:$\displaystyle R=\frac{\mathrm{avg}(L_1)}{\mathrm{avg}(L_1,L_2)}$,其中 $\mathrm{avg}(L_1)$ 表示原始信息经过信源编码后的平均码长,$\mathrm{avg}(L_1,L_2)$ 表示原始信息经过信源和信道两层编码后的平均码长。
例如:假设原始信息是等概率的 ${A,B,C}$,我们用 ${0,10,11}$ 对其进行信源编码,那么平均码长为 $\frac{1+2+2}{3}=\frac{5}{3}$;接着,我们使用三重重复码(即将每个比特重复三次)再对其进行信道编码,那么平均码长变为 $\frac{3+6+6}{3}=5$,因此信道传输速度为 $R=\frac{5/3}{5}=\frac{1}{3}$。
信道容量和信道传输速度间的关系由著名的 $\mathrm{Shannon}$ 第二定理,又称信道编码定理给出。它指出:只要信道传输速率 $R\le C$,就存在一种编码方式,使得误码率可以任意小(只要码长足够长);反之,如果 $R>C$,则任何编码方式的误码率都有一个不为零的下限。
直观上看,噪声越少的信道,其信道容量 $C$ 越大,因此允许的信道传输速率 $R$ 也就越大(即在信道编码中可以引入更少的冗余来保证传输的可靠性);反之,噪声越大的信道,其信道容量 $C$ 越小,因此允许的信道传输速率 $R$ 也就越小(即在信道编码中必须引入更多的冗余来保证传输的可靠性)。
$\mathrm{Shannon}$ 第二定理本身的证明比较复杂,这里就不再赘述了。有兴趣的同学可以参考文末的阅读材料,或者直接阅读 $\mathrm{Shannon}$ 的原始论文《A Mathematical Theory of Communication》。这篇论文是整个信息论的奠基之作,其完整性甚至到今天还能作信息论教材使用,再怎么赞美都不为过。
四、信息论的扩展与应用
受 $\mathrm{Shannon}$ 信息论的启发,后续的研究者们提出了很多用于度量概率分布间距离的指标。这些指标至今仍在人工智能和概率统计领域有着广泛的应用。
4.1 分布间距离的度量
在这些指标中,最著名的莫过于交叉熵:$\displaystyle H(P,Q)=-\sum_x P(x)\log Q(x)$,它衡量了按照概率分布 $Q$ 的最优编码对真实分布为 $P$ 的信息进行编码的平均码长。在给定 $P$ 的情况下,如果 $Q$ 和 $P$ 越接近,交叉熵越小;如果 $Q$ 和 $P$ 越远,交叉熵就越大。
容易发现,交叉熵的绝对大小与 $Q$ 本身的熵有关。为了消除这个影响,我们可以定义相对熵(又称 $\mathrm{Kullback–Leibler(KL)}$ 散度):$\displaystyle KL(P,Q)=H(P,Q)-H(P)=-\sum_x P(x)\log\left(\frac{Q(x)}{P(x)}\right)$。$\mathrm{KL}$ 散度总是非负的,它衡量了使用 $Q$ 对 $P$ 进行编码时所引入的额外码长。
然而,$\mathrm{KL}$ 散度并不满足对称性。**$\mathrm{Jensen-Shannon(JS)}$ 散度**是 $\mathrm{KL}$ 散度的一种改进,其定义为:$JS(P,Q)=\frac{1}{2}KL\left(P,\frac{P+Q}{2}\right)+\frac{1}{2}KL\left(Q,\frac{P+Q}{2}\right)$。它解决了 $\mathrm{KL}$ 散度不对称的问题,但这两个散度都存在一个问题:如果两个分布没有重叠或者重叠非常少时,散度值会变得非常大,甚至趋于无穷大,这在实际应用中并不理想。
为了解决这个问题,研究者们提出了 $\mathrm{Wasserstein}$ 距离。它的形式化定义比较复杂,但可以直观地理解为:如果将两个分布看作两个土堆,那么 $\mathrm{Wasserstein}$ 距离就是将一个土堆变成另一个土堆所需搬运的最小工作量。就比如下图所示:
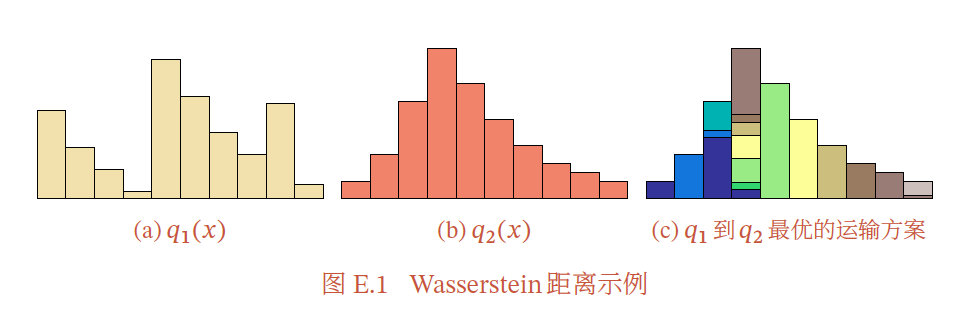
$\mathrm{Wasserstein}$ 距离相较 $\mathrm{KL}$ 散度和 $\mathrm{JS}$ 散度的优势在于:即使两个分布没有重叠或者重叠非常少,$\mathrm{Wasserstein}$ 距离仍然能反映两个分布的远近。
4.2 信息论在人工智能中的应用
前面提到,信息论中的这些分布间距离度量的指标在人工智能领域有着广泛的应用。例如,机器学习中最常用的损失函数之一交叉熵损失函数就是基于交叉熵定义的;又例如,今年年初爆火的 $\mathrm{DeepSeek-R1}$ 模型所使用的 $\mathrm{GRPO}$ 算法中就包含了 $\mathrm{KL}$ 散度惩罚项,用于稳定强化学习训练过程。
此外,在生成式模型中,由于需要衡量生成分布和真实数据分布之间的差异,信息论中的这些指标也被广泛使用。例如:在生成对抗网络($\mathrm{GAN}$)中,原始的 $\mathrm{GAN}$ 使用 $\mathrm{JS}$ 散度来衡量生成分布和真实数据分布之间的差异;而后续的 $\mathrm{Wasserstein}$ $\mathrm{GAN}$ 则使用 $\mathrm{Wasserstein}$ 距离来替代 $\mathrm{JS}$ 散度,从而提升了训练的稳定性和生成样本的质量。
信息熵本身也在人工智能的学术前沿有着一席之地。众所周知,大模型的最终输出是从一个概率分布中采样得到的,而信息熵正是衡量这个概率分布不确定性的一个重要指标。一个质量更高的回答应当具有更高还是更低的信息熵,至今仍然是一个开放性的问题。
关于人工智能的更多内容,敬请期待本学期后续的《肆叁小灶》系列推送。
阅读材料
- C. E. Shannon, “A Mathematical Theory of Communication”
- Stefan M. Moser, “A Student’s Guide to Coding and Information Theory”
- 邱锡鹏,《神经网络与深度学习》nndl.github.io