肆叁小灶第五讲 数据结构预备知识（下）

肆叁小灶第五讲，介绍了数据结构相关的树论知识。

笃实 43 班的同学们大家好。本期推送我们将接着上期的内容，介绍一些树论相关的知识。

一、树的基本概念

树在《数据结构》和《离散数学（2）》中的定义略有不同且较为复杂，这里我们分开讨论。

对于无向图，无环的无向图称为无向森林，简称森林，无向森林中的每个连通分量称为一棵无向树，简称树。树有两个重要性质：一是树中任意两个顶点之间有且仅有一条路径；二是 $n$ 个顶点的树恰好有 $n-1$ 条边。

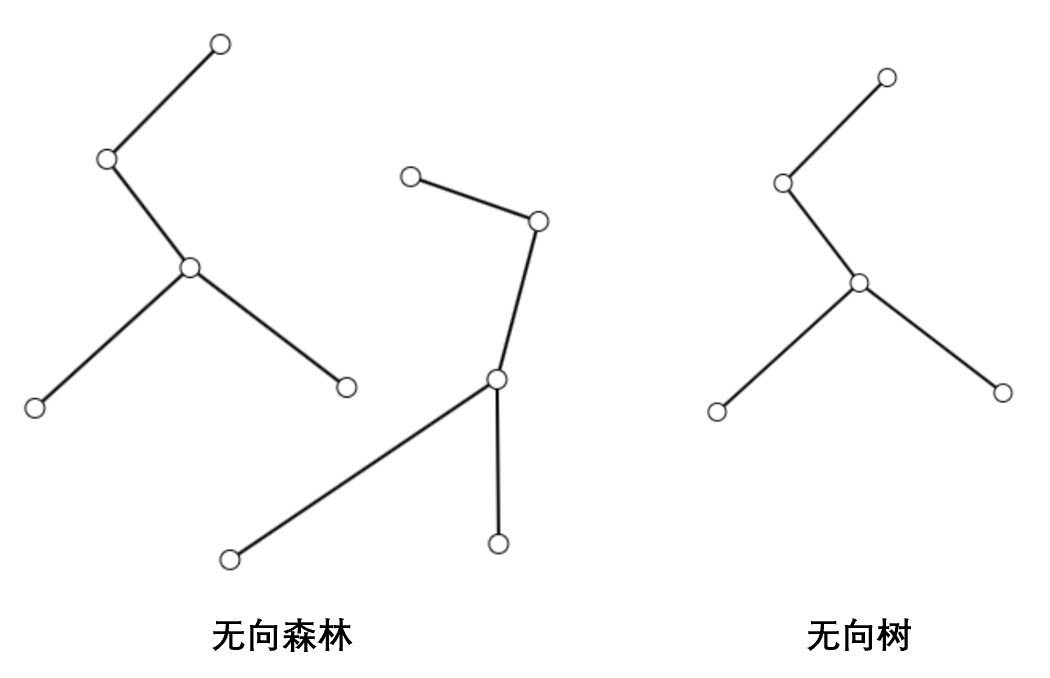
我们可以采用上期介绍的 BFS 来遍历树。任意选中一个顶点作为起点，由于树中任意两个顶点之间有且仅有一条路径，我们可以按照到起点的路径长度从小到大排列每个顶点，从而把树的顶点分为若干层。此时若将每条边加上从上层指向下层的方向，我们就得到了一个有向根树，简称根树。

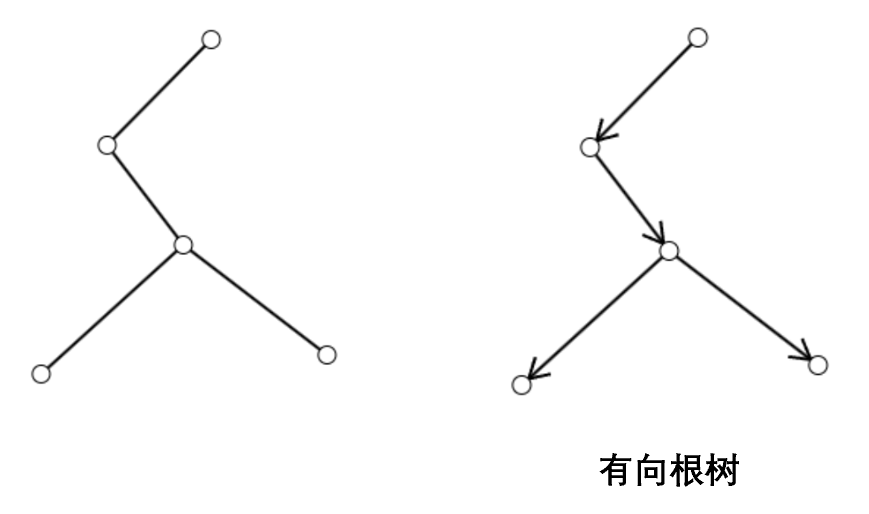
在根树中，我们称一条路径为链路。入度为 $0$ 的顶点称为根节点，出度为 $0$ 的顶点称为叶节点，其余顶点称为内部节点；对于一条有向边 $(a,b)$，我们称 $a$ 是 $b$ 的父节点，$b$ 是 $a$ 的子节点。类似地，我们可以定义兄弟、堂兄弟、祖父、祖先、后代等概念。

对于根树中的每个节点，定义其深度为从根节点到该节点的路径长度，定义其高度为从该节点到其所有后代的最长路径长度。事实上，根树中的一个节点与其所有后代也构成了一棵根树，我们称其为该节点的子树。定义根树的高度为其根节点的高度。

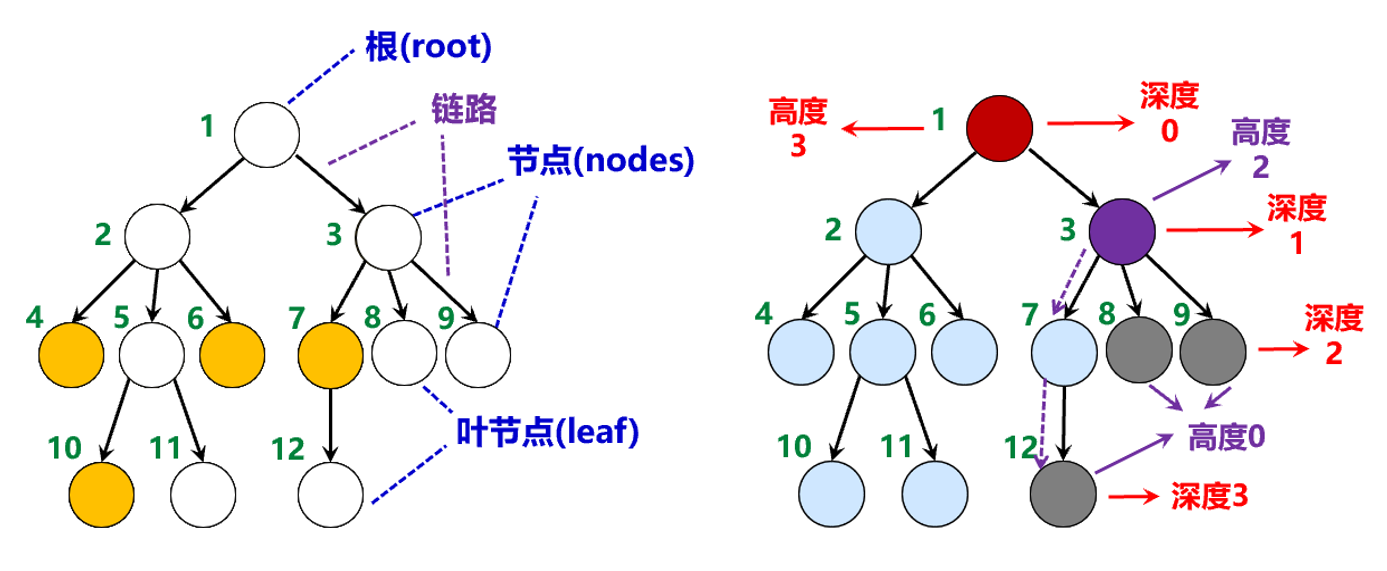
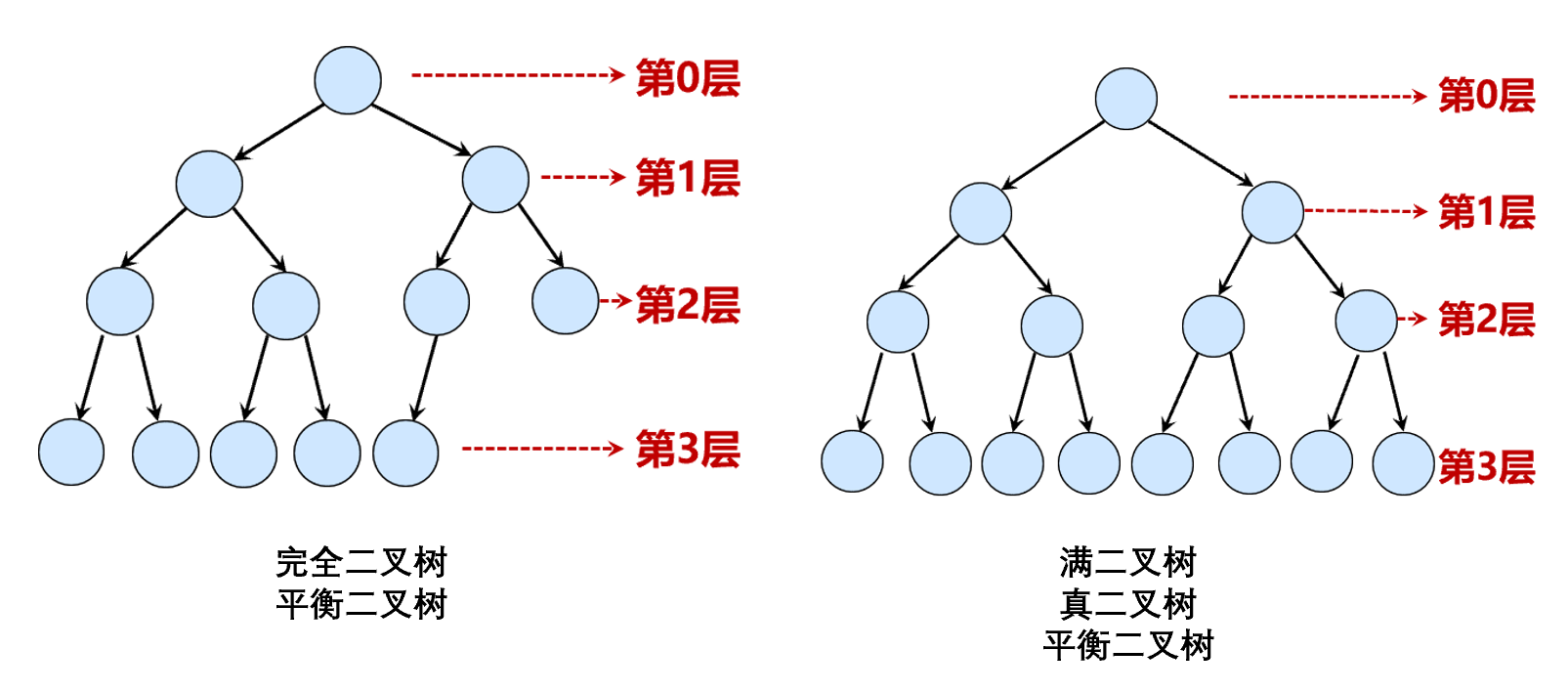
如果一棵根树中每个节点至多有 $k$ 个子节点，则称其为 $k$ 叉树；对于二叉树（即 $k=2$ 的 $k$ 叉树），我们可以定义除叶节点外每个节点的左孩子与右孩子，并且可以定义满二叉树（除叶节点外每个节点都有两个子节点）、完全二叉树（除了最后一层外每层都满且不存在只有右孩子而没有左孩子的节点）、真二叉树（不存在只有一个孩子的节点）、平衡二叉树（任意节点的左右子树高度差不超过 $1$）等概念。

更普遍地，对于一个有向无环图，如果不考虑其边的方向时，其也不存在环，我们称其为一个有向森林，有向森林中的每个弱连通分量称为一棵有向树。若一个有向树有且仅有一个入度为 $0$ 的节点且每个节点的入度不超过 $1$，则其就是前文所说的根树；其他有向树则称为有向无根树，简称无根树。

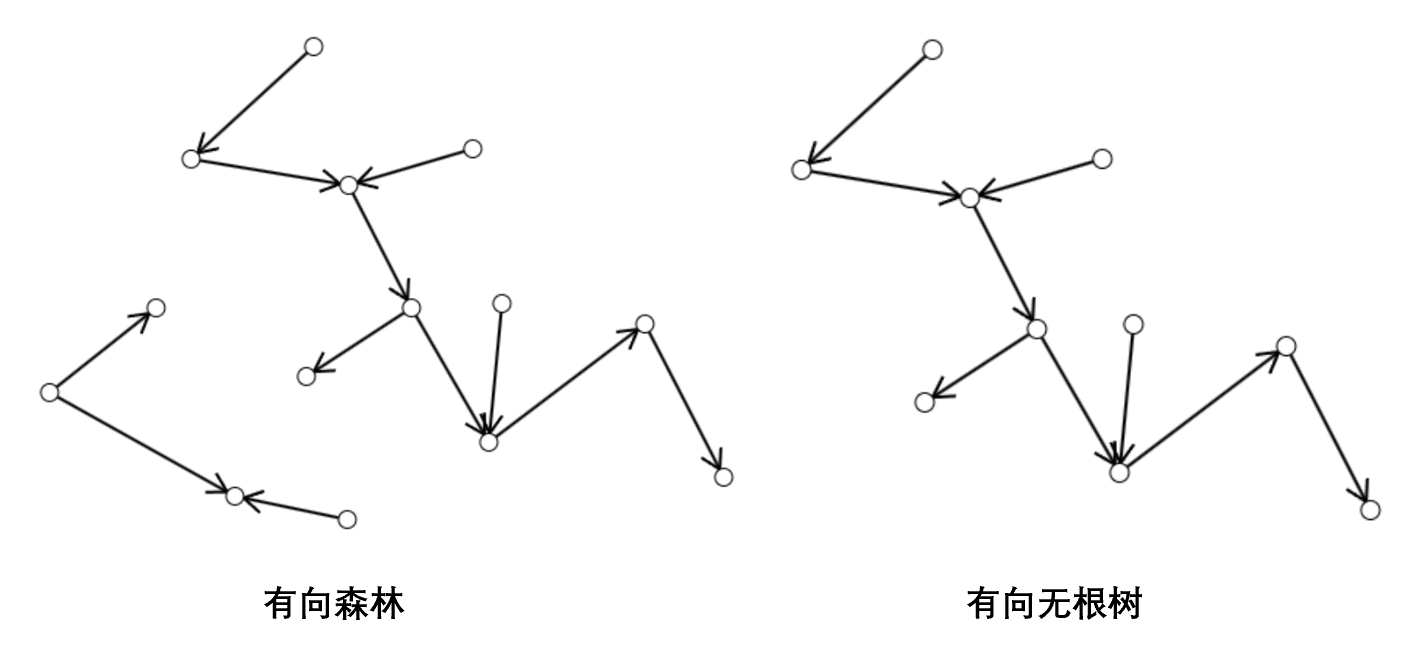
无根树在数据结构中的应用不多，但在树论中极其重要，可以用于求解图中支撑树的数量，以及图的回路和割集。但其证明过程十分冗长，且需要用到大量线性代数和图论的知识，可以说是整个《离散数学（2）》中最复杂的部分。由于篇幅所限，此处就不展开了。感兴趣的同学欢迎选修《离散数学（2）》。

二、树的表示与遍历

根树主要有两种表示方法：父亲-孩子表示法和长子-兄弟表示法。

在父亲-孩子表示法中，每个节点存储其自身属性（一般指权值与颜色等）、指向其父节点的指针以及指向其所有子节点的指针数组。可以发现，这其实和有向图的邻接表类似。下面是一个例子：

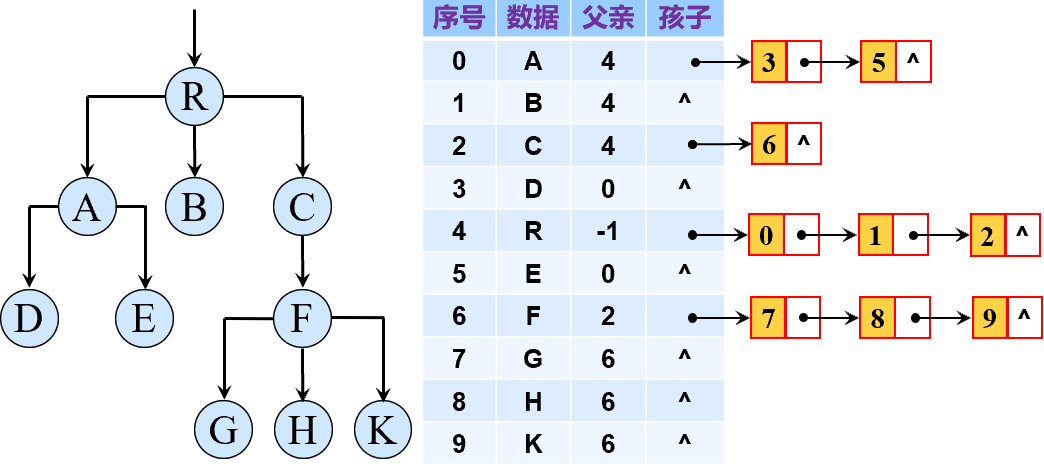
在长子-兄弟表示法中，每个节点存储其自身属性、指向其长子的指针以及指向其下一兄弟的指针。相较于父亲-孩子表示法，长子-兄弟表示法更节省空间。下面是一个例子：

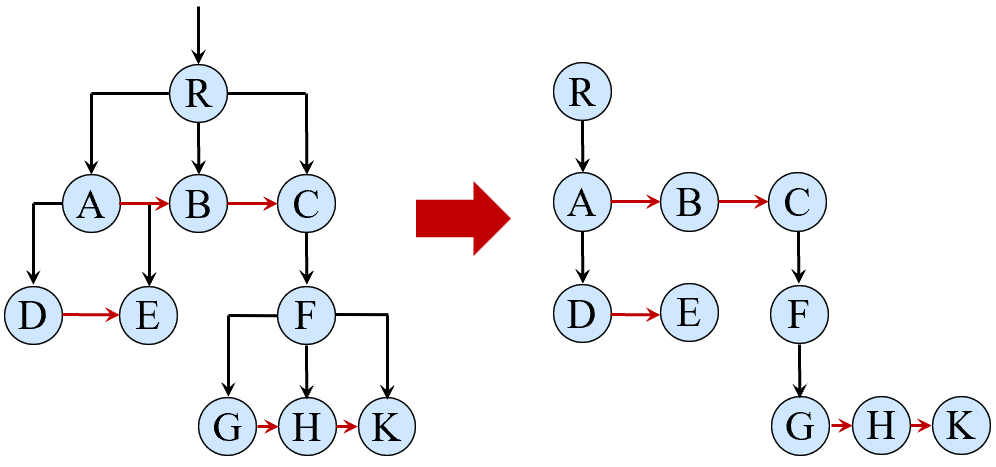
利用长子-兄弟表示法，我们可以将任何一棵根树转化为二叉树：只需要把长子看作左孩子，把下一兄弟看作右孩子即可。此外，二叉树也可以转化为多叉树：对二叉树中的每个节点，增加其到其左孩子的右孩子（及后续右孩子）的链路，再删除所有右链路即可。下面是一个例子：

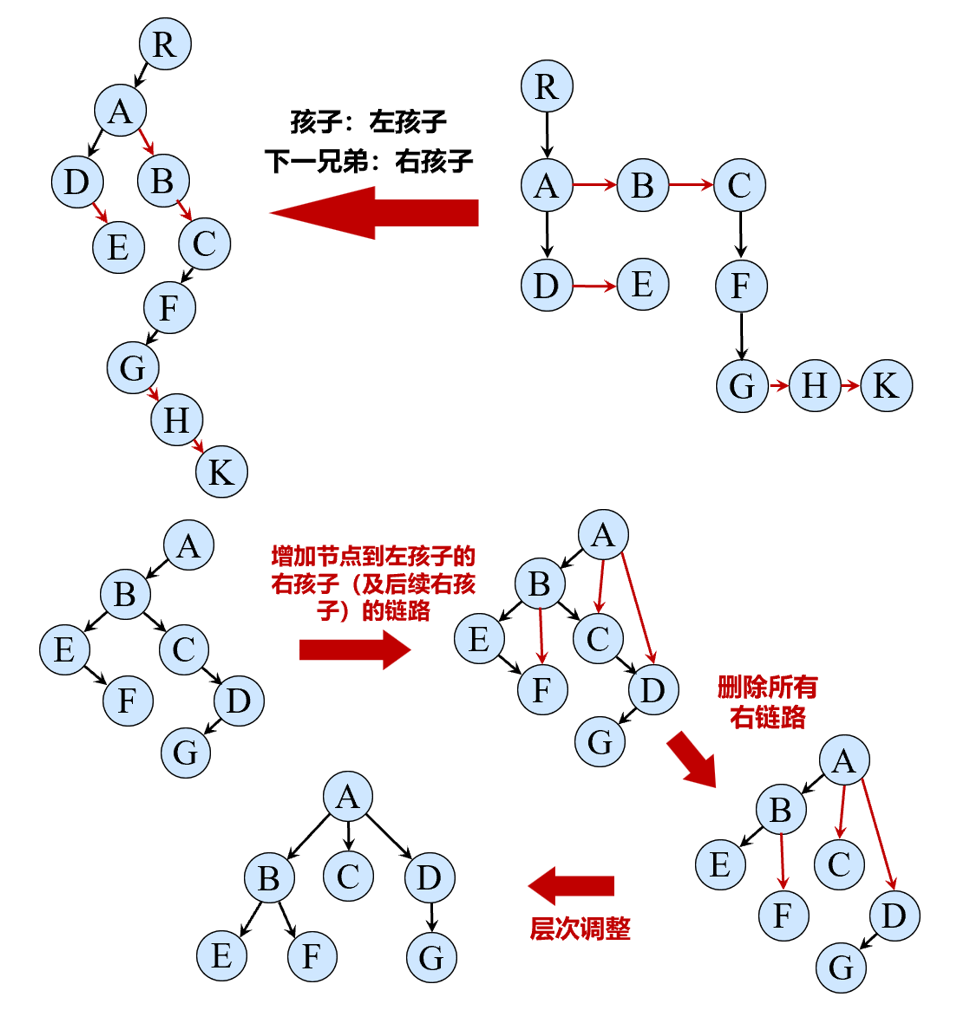
而对于森林，可以把森林中每棵树的根都看作兄弟，从而也可以转化为二叉树。因此，二叉树虽然是根树和森林的特殊情况，但其表达能力是相同的，且更简洁、计算效率更高。因此，在《数据结构》中，通常只研究二叉树。

二叉树有其自己的表示方法：顺序表示法。对于一个 $n$ 层的二叉树，我们可以先将其补全为完全二叉树，然后将其按照从上到下、从左到右的顺序编号。编完号后，再将补全的节点删除，我们就得到了原二叉树的顺序表示。下面是一个例子：

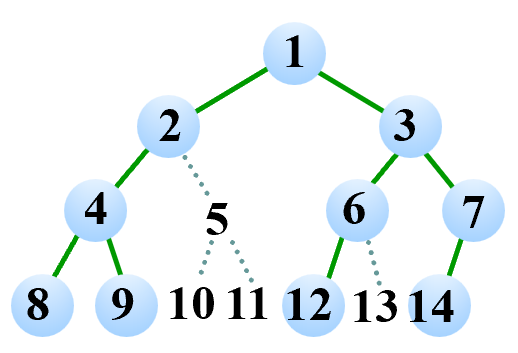
但这种方法空间利用率较低，尤其是对于右孩子较多而左孩子较少的二叉树。因此在实际应用中，我们通常还是使用父亲-孩子表示法。

二叉树的遍历方法主要有三种：前序遍历、中序遍历和后序遍历。前序遍历是先访问根节点，再访问左子树，最后访问右子树；中序遍历是先访问左子树，再访问根节点，最后访问右子树；后序遍历是先访问左子树，再访问右子树，最后访问根节点。事实上，这三种方法都是从上期介绍的 DFS 方法演化而来的。下面是基于父亲-孩子表示法的三种遍历的伪代码：

void PreOrder(Node* root) { // 前序遍历
    if (root == nullptr) return; // 如果节点为空，直接返回
    cout << root->value << " "; // 访问根节点
    for (Node* child : root->children) { // 遍历所有子节点
        PreOrder(child); // 递归访问子节点
    }
}
void InOrder(Node* root) { // 中序遍历
    if (root == nullptr) return; // 如果节点为空，直接返回
    if (!root->children.empty()) { // 如果有子节点
        InOrder(root->children[0]); // 递归访问第一个子节点
    }
    cout << root->value << " "; // 访问根节点
    for (int i = 1; i < root->children.size(); ++i) { // 遍历剩余子节点
        InOrder(root->children[i]); // 递归访问子节点
    }
}
void PostOrder(Node* root) { // 后序遍历
    if (root == nullptr) return; // 如果节点为空，直接返回
    for (Node* child : root->children) { // 遍历所有子节点
        PostOrder(child); // 递归访问子节点
    }
    cout << root->value << " "; // 访问根节点
}

此外，还可以仿照上期介绍的 BFS 方法，定义层序遍历：从根节点开始，先访问根节点，再访问其所有子节点，再访问其所有孙子节点。下面是基于父亲-孩子表示法的层序遍历的伪代码：

void LevelOrder(Node* root) { // 层序遍历
    if (root == nullptr) return; // 如果节点为空，直接返回
    queue<Node*> q; // 创建一个队列
    q.push(root); // 将根节点入队
    while (!q.empty()) { // 当队列不为空时
        Node* node = q.front(); // 取出队首节点
        q.pop(); // 出队
        cout << node->value << " "; // 访问当前节点
        for (Node* child : node->children) { // 遍历所有子节点
            q.push(child); // 将子节点入队
        }
    }
}

如果觉得看代码有些晦涩，下面是一个具体的例子：

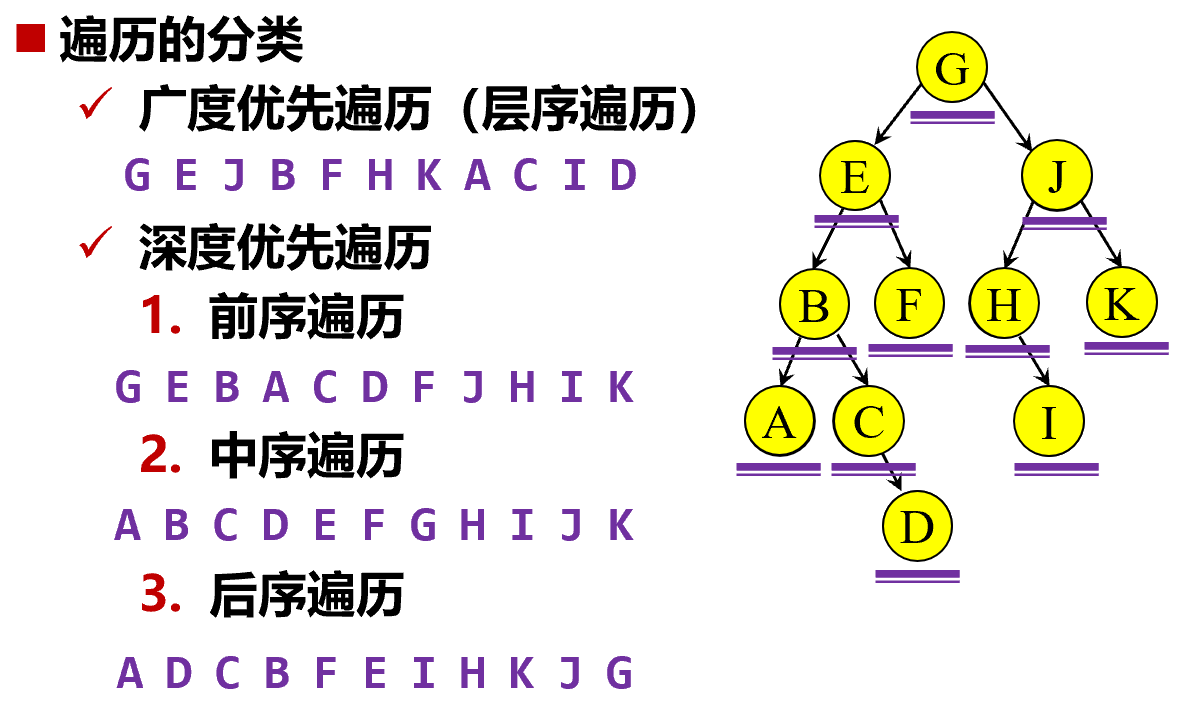
三、树论算法简介

1. 最优二叉树

将一个完全二叉树的所有叶节点都赋予权重，我们称其为赋权二叉树。定义赋权二叉树的带权路径长度为其所有叶节点的权值与其深度的乘积之和。在叶节点个数以及它们对应的权值相同的情况下，构造出的所有赋权二叉树中带权路径长度最短的树即称为最优二叉树。最优二叉树通常采用 Huffman 算法构造。

Huffman 算法的基本思想是：每次从所有叶节点中选取权值最小的两个叶节点，将它们合并为一个新节点，并将新节点的权值设为这两个叶节点的权值之和，直到只剩下一个节点为止。下面是一个例子：

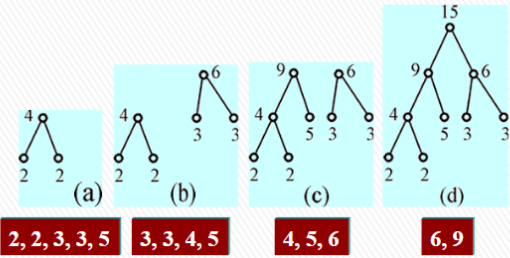
最优二叉树的应用非常广泛，尤其是在数据压缩领域。它可以用于构造最优的前缀编码（即 Huffman 编码），使得编码后的数据量最小。Huffman 编码在《数据结构》课程中会详细介绍，此处就不展开了。

2. 最小支撑树

支撑树是指无向图的无环连通支撑子图。最小支撑树就是一个图的所有支撑树中边权和最小的支撑树。最小支撑树有两种常用的算法：Prim 算法和 Kruskal 算法。

Prim 算法与上期介绍的 Dijkstra 算法有一些类似：都是从一个顶点开始，逐步扩展到其他顶点。具体地，Prim 算法从一个顶点开始，逐步将与当前支撑树相连的最小边加入支撑树，直到所有顶点都被包含在支撑树中。下面是一个例子：

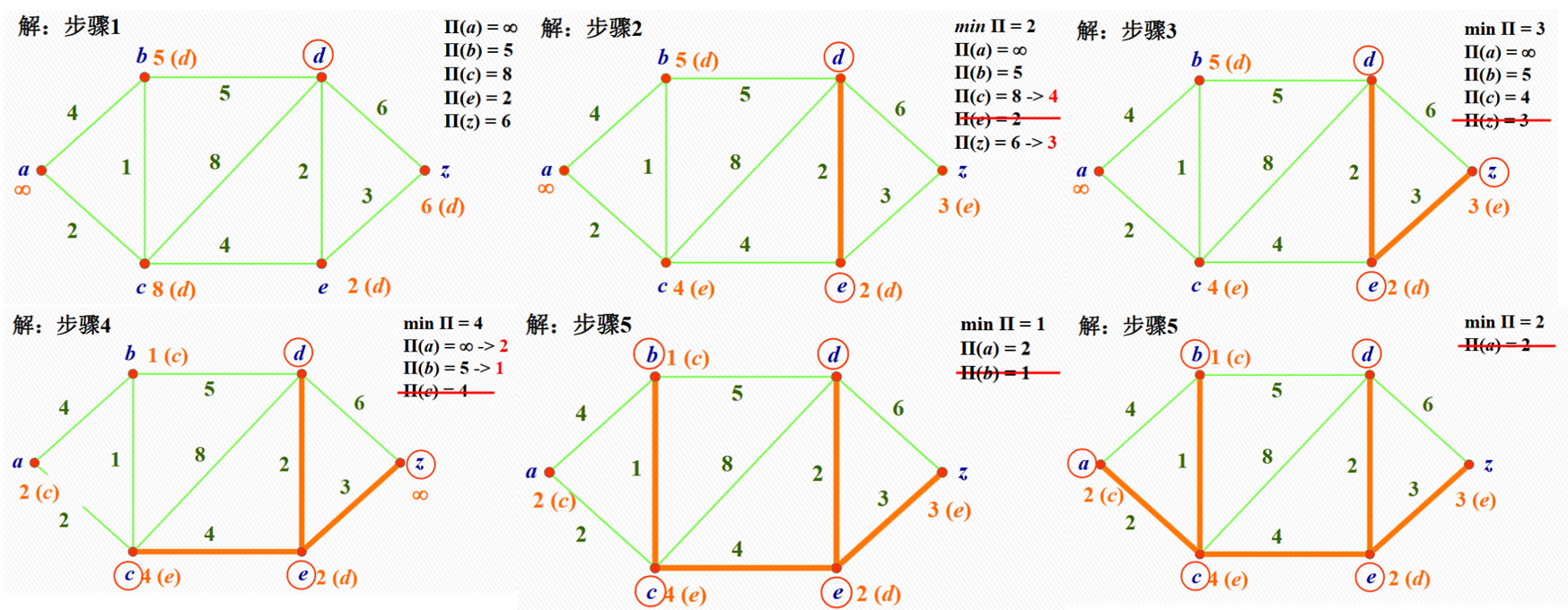
下面是基于邻接表的 Prim 算法的伪代码：

void Prim(int start, vector<vector<pair<int, int>>>& adj) {
    int n = adj.size(); // 图的顶点数
    vector<bool> visited(n, false); // 记录顶点是否被访问
    vector<int> minEdge(n, INT_MAX); // 记录每个顶点到支撑树的最小边权
    minEdge[start] = 0; // 起始顶点到支撑树的边权为 0
    int totalWeight = 0; // 支撑树的总边权

    for (int i = 0; i < n; ++i) {
        int u = -1; // 当前选中的顶点
        for (int j = 0; j < n; ++j) {
            if (!visited[j] && (u == -1 || minEdge[j] < minEdge[u])) {
                u = j; // 找到未访问的最小边权顶点
            }
        }
        visited[u] = true; // 标记当前顶点为已访问

        for (auto& edge : adj[u]) { // 遍历当前顶点的所有邻接顶点
            int v = edge.first;
            int weight = edge.second;
            if (!visited[v] && weight < minEdge[v]) {
                minEdge[v] = weight; // 更新邻接顶点到支撑树的最小边权
            }
        }
    }
}

Kruskal 算法则更为直观：它从所有边中选取权值最小的边，如果加入该边后不会形成环（即该边的两个顶点不在同一个连通分量中），则将其加入支撑树，并将该边的两个顶点所在的连通分量合并，直到所有顶点都被包含在支撑树中。可见，Kruskal 算法执行过程中需要频繁进行“合并”和“查找”操作，这就需要使用一种叫做并查集的数据结构来高效地实现。

并查集的思想非常简单：我们将每个顶点看作一个独立的集合，初始时每个顶点都是一个单独的集合。每次合并两个集合时，我们只需要将其中一个集合的代表元素指向另一个集合的代表元素即可。查找操作则是沿着代表元素的指针一直向上查找，直到找到根节点为止。下面是并查集基本操作的伪代码：

int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]); // 路径压缩
    }
    return parent[x]; // 返回根节点
}
void union(int x, int y) {
    int rootX = find(x); // 查找 x 的根节点
    int rootY = find(y); // 查找 y 的根节点
    if (rootX != rootY) {
        parent[rootY] = rootX; // 将 y 的根节点指向 x 的根节点
    }
}

基于邻接表的 Kruskal 算法的伪代码如下：

void Kruskal(vector<pair<int, pair<int, int>>>& edges, int n) {
    sort(edges.begin(), edges.end()); // 按边权从小到大排序
    vector<int> parent(n); // 初始化并查集
    for (int i = 0; i < n; ++i) {
        parent[i] = i; // 每个顶点的父节点指向自己
    }
    vector<pair<int, int>> mst; // 存储最小支撑树的边
    for (auto& edge : edges) {
        int weight = edge.first; // 边权
        int u = edge.second.first; // 边的起点
        int v = edge.second.second; // 边的终点
        if (find(u) != find(v)) { // 如果 u 和 v 不在同一个连通分量中
            union(u, v); // 合并 u 和 v 的连通分量
            mst.push_back({u, v}); // 将边加入最小支撑树
        }
    }
}

四、树的应用

这里给出一道有趣的算法题：

对于一个正权无向简单连通图，定义两点间某条路径的强度为路径上所有边权的最小值，定义两点间的距离为两点间所有路径强度的最大值。

如两点间的某条路径由 $3$ 条边组成，边权分别为 $2,3,5$，则该路径的强度为 $2$；若该两点间只有两条路径，且另外一条路径的强度是 $4$，则该两点间的距离为 $\max(2,4)=4$。

请设计一个算法，求出该图的一个支撑子图，使其满足以下要求：（1）该支撑子图连通；（2）该支撑子图中两点间的最小距离最大；（3）在满足（1）（2）的条件下，总边数最少。

以下伪代码是该问题的一个可行解，采用了类似 $\mathrm{Kruskal}$ 的思想，请阅读并完成填空：

int find(int n){
    while(n != parent[n]) {
        ____________(1)
    }
    return n;
}
void union(int x,int y){
    parent[x]=parent[y];
}
int main(){
    for(int i=1;i<=edges.num;i++)
        for(int j=i+1;j<=edges.num;j++)
            if(____________(2))
                swap(edges[i], edges[j]);
    blocks_cnt=n;
    for(int i=1;i<=edges.num;i++){
        int x=find(edges[i].start);
        int y=find(edges[i].end);
        if(x != y) {
            ____________(3)
            blocks_cnt--;     
        }
        if(__________(4)){
            print("%d",__________(5));
            return 0;
        }
    }
}

本题的解法就不在此处直接给出了，感兴趣的同学可以尝试自己完成。这里给出一个提示：可以尝试证明，满足上述三个要求的支撑子图一定是原图的一棵支撑树。

《数据结构预备知识》系列推送就到此结束了。希望同学们能在本系列推送中有所收获，也祝同学们在接下来小学期的《程序设计实训》课程中一帆风顺。