肆叁小灶第四讲 数据结构预备知识（上）

肆叁小灶第四讲，介绍了数据结构相关的图论知识。

笃实 43 班的同学们大家好。下学期大部分同学都将修读《数据结构》，但由于笃实书院教学计划将《离散数学（2）》放在了大二下学期，因此大部分同学可能还未接触过图论与树论相关的知识。为了帮助大家更好地学习《数据结构》，我们将介绍一些预备知识。由于篇幅所限，我们将内容分为上下两期，本期主要介绍图论，下期主要介绍树论。

一、图的基本概念

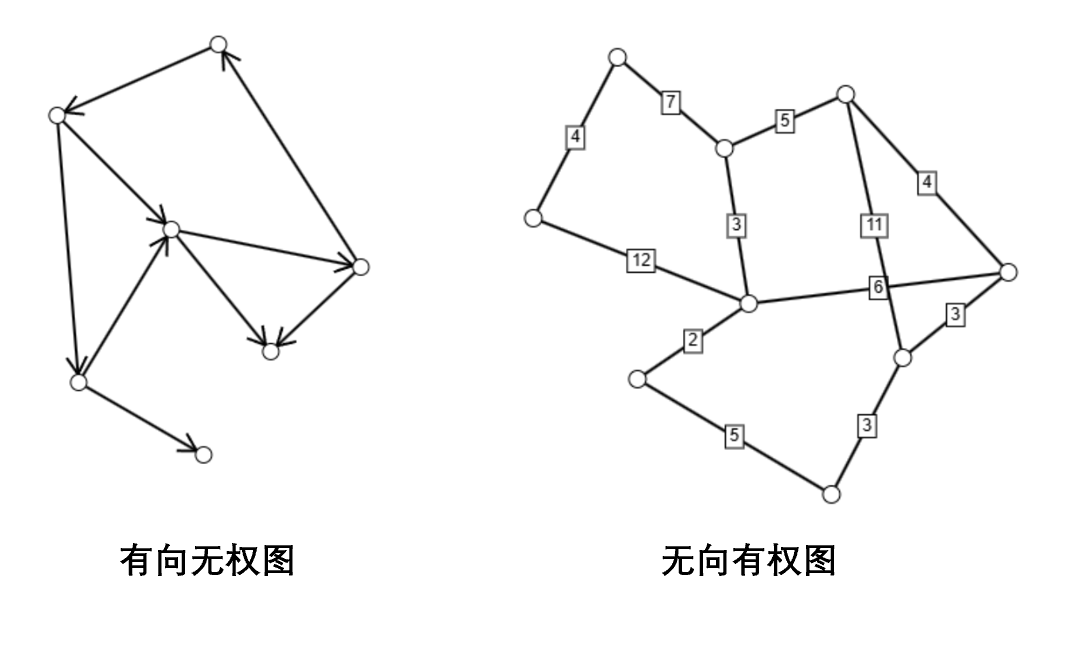
图是由顶点和边组成的集合，通常用 $G=(V,E)$ 表示，其中 $V$ 是顶点集，$E$ 是边集。图可以是有向的或无向的，有向图中的边有方向，而无向图中的边没有方向；同时，也可以按边是否带有权值分为带权图和无权图。在无向图中，我们定义一个顶点的度数为与该顶点相连的边的数量。对于有向图，顶点的入度是指指向该顶点的边的数量，出度是指从该顶点出发的边的数量。

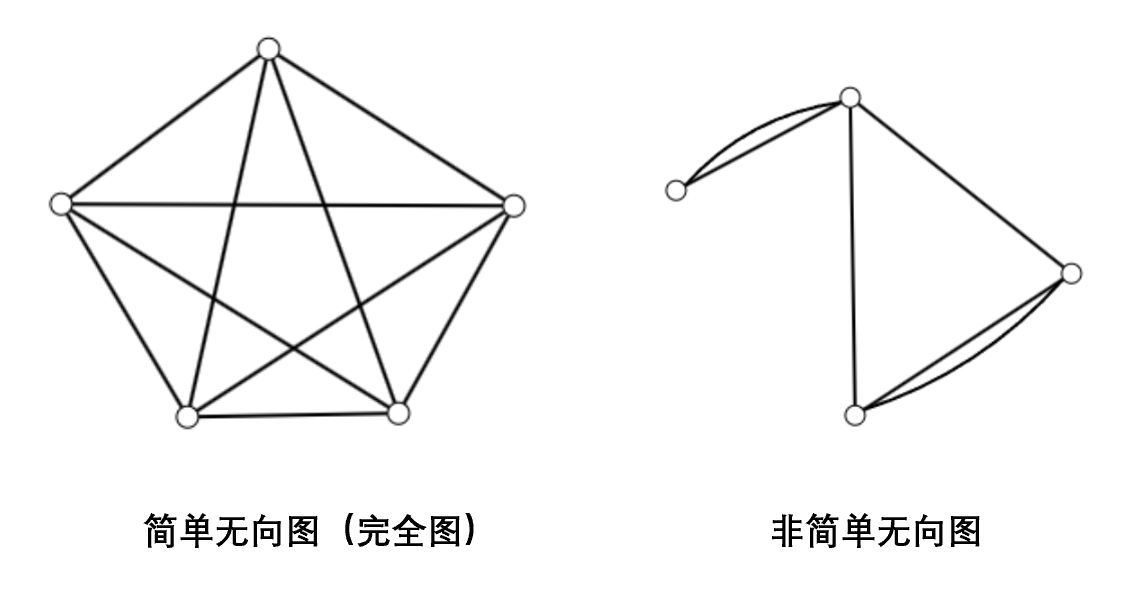
如果一个无向图中既不带有从一个顶点指向其自身的边（即无自环），且任意两个顶点之间至多只有一条边（即无重边），则称之为简单无向图。若一个简单无向图中，任意两个顶点之间都有一条边，则称之为完全图。

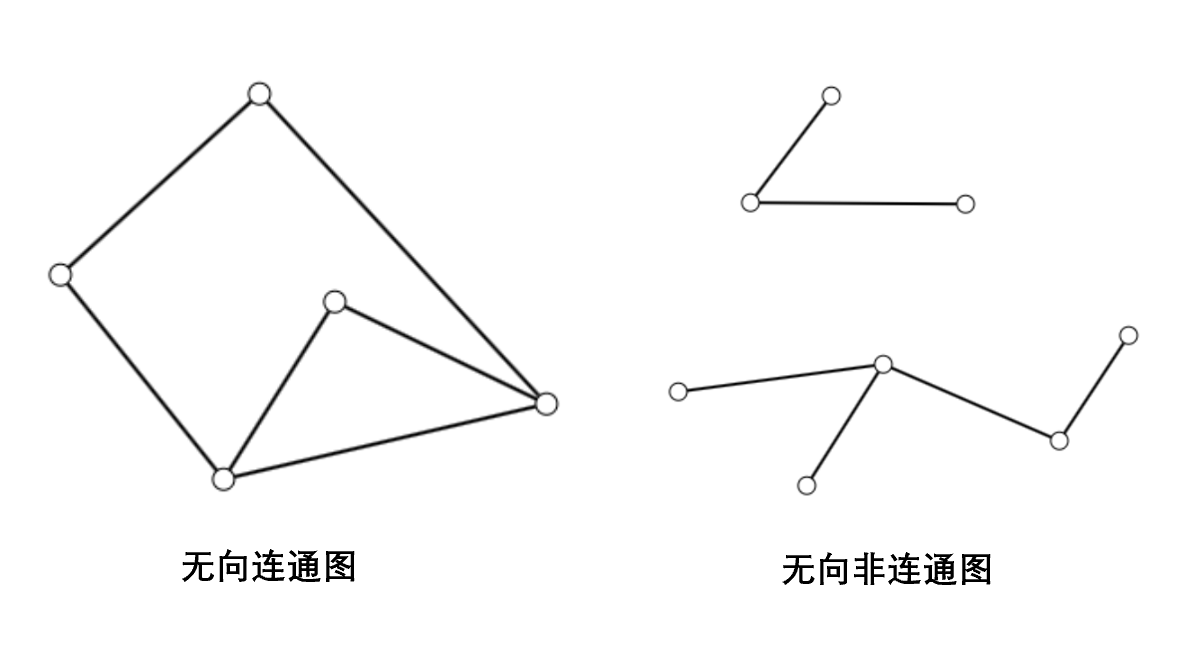
图的连通性在有向图和无向图上的定义略有不同：在无向图中，若两个顶点间存在一条路径，则称这两个顶点是连通的；若图中任意两个顶点都是连通的，则称该图是无向连通图。

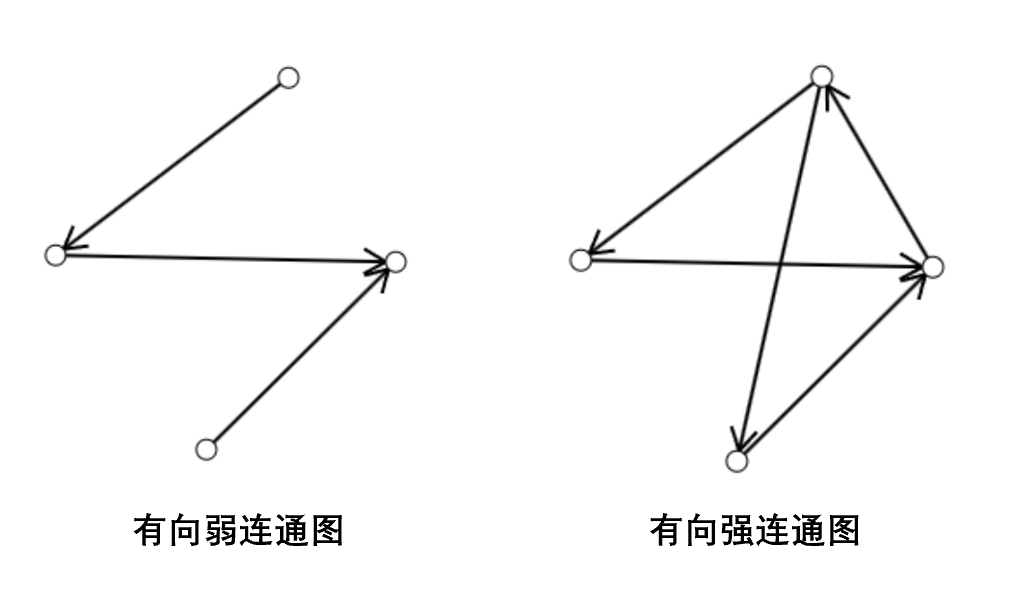
在有向图中，边存在方向。如果我们先不考虑边的方向（即把有向图看作无向图），此时若两个顶点连通，则称这两个顶点弱连通；如果考虑边的方向，此时若两个顶点间只存在从一个顶点到另一个顶点的路径而不存在反向路径，则称这两个顶点单向连通；如果两个方向的路径都存在，则称这两个顶点强连通。和无向图一样，我们可以定义有向弱连通图和有向强连通图。

图是顶点和边的集合，既然集合里有子集的概念，图里自然也有子图的概念。子图是指从原图中选取部分顶点和边构成的图。若子图包含原图的所有顶点，则称之为支撑子图。

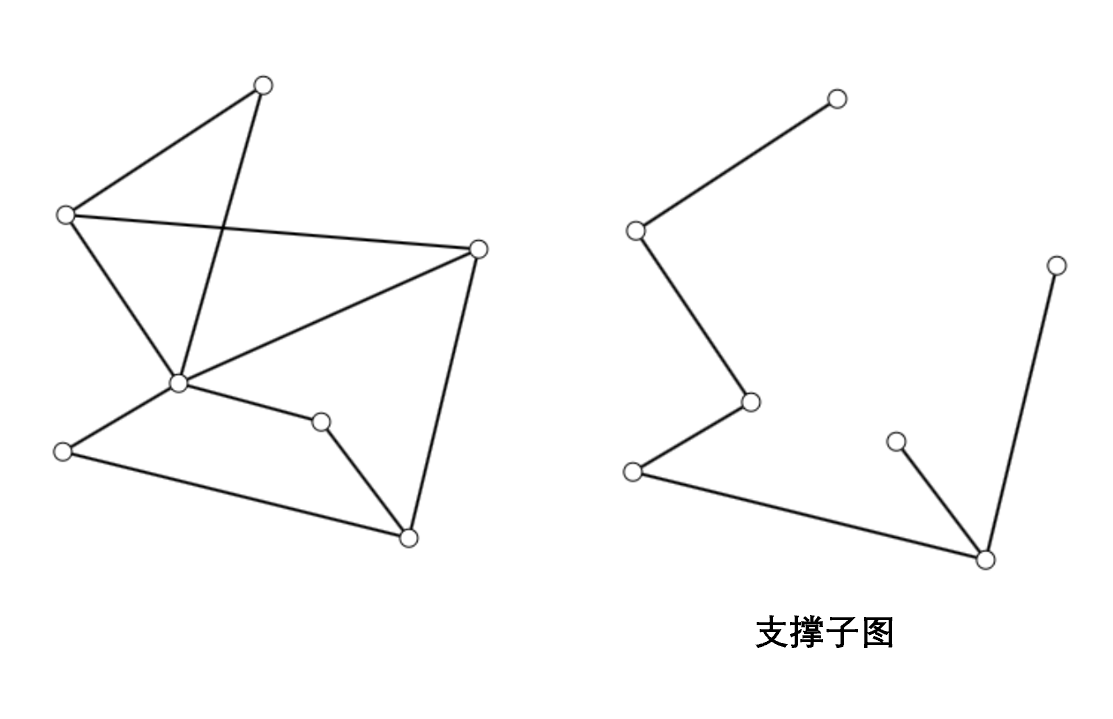
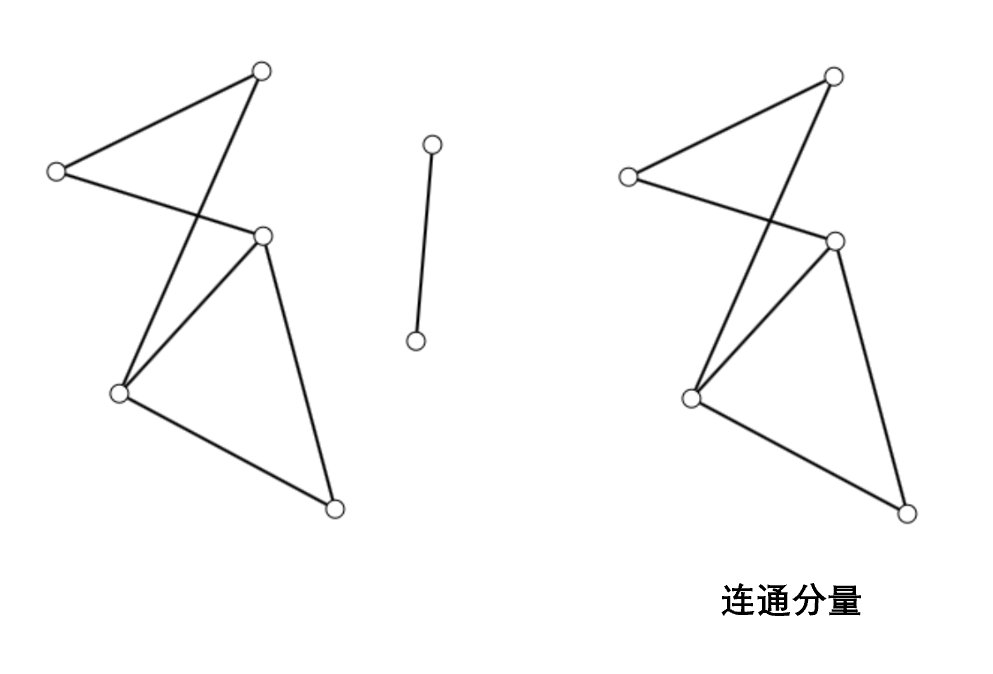
在无向图中，若某个连通的子图是“极大”的（即不是任何连通子图的真子图），则称之为原图的一个连通支或连通分量。对于有向图，类似地，我们可以定义有向图的强连通分量。

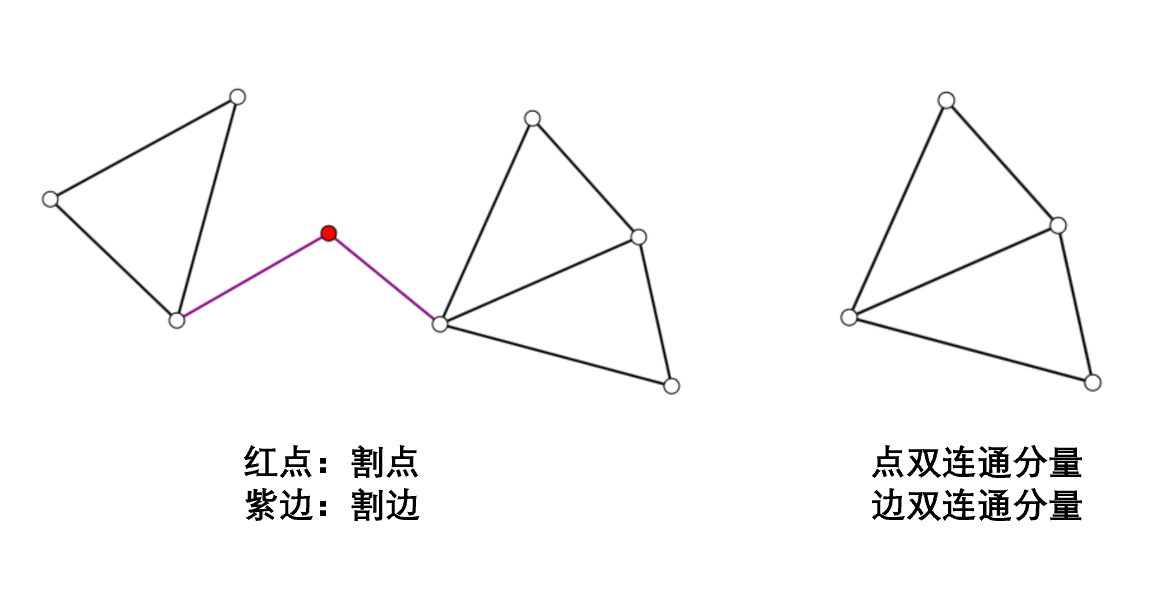
对每个无向图，我们都可以统计其连通支的个数。如果去除原图中的某条边后，图的连通支个数增加了，则称这条边为割边；如果去除某个顶点后，图的连通支个数增加了，则称这个顶点为割点。没有割点的极大连通子图称为一个点双连通分量；没有割边的极大连通子图称为一个边双连通分量。

二、图的表示与遍历

图的表示方法有很多种，常见的有邻接矩阵和邻接表。

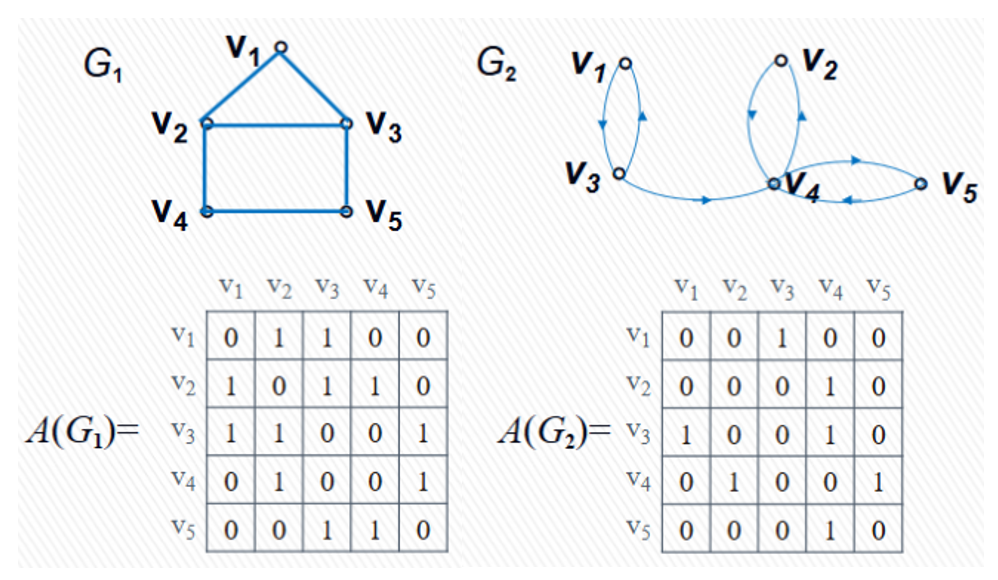
邻接矩阵是一个 $n \times n$ 的矩阵，其中 $n$ 是图的顶点数。若顶点 $i$ 和顶点 $j$ 之间存在边，则矩阵中对应位置的值为 $1$（或边的权值），否则为 $0$（或无穷大）。

邻接表是一个数组，其中每个元素是一个链表或动态数组，表示与该顶点相连的所有顶点。相较于邻接矩阵，邻接表往往更节省空间，且便于访问某个顶点的邻接顶点，在进行图的遍历时更为高效，因此在实际应用中更为常用。

图的遍历方法主要有两种：深度优先搜索（DFS）和广度优先搜索（BFS）。

深度优先搜索（DFS）是从一个顶点开始，沿着一条路径尽可能深入，直到无法继续为止，然后回溯到上一个顶点，继续探索其他路径。DFS 可以使用递归或栈来实现，下面是一个简单的基于邻接表的 DFS 遍历伪代码：

void DFS(int v, vector<bool>& visited, vector<vector<int>>& adj) {
    visited[v] = true; // 标记当前顶点为已访问
    cout << v << " "; // 访问当前顶点

    for (int u : adj[v]) { // 遍历当前顶点的所有邻接顶点
        if (!visited[u]) { // 如果邻接顶点未被访问
            DFS(u, visited, adj); // 递归访问邻接顶点
        }
    }
}

广度优先搜索（BFS）是从一个顶点开始，首先访问该顶点，然后访问所有与该顶点直接相连的顶点，再访问这些顶点的邻接顶点，以此类推，直到所有可达顶点都被访问。BFS 通常使用队列来实现，下面是一个简单的基于邻接表的 BFS 遍历伪代码：

void BFS(int start, vector<bool>& visited, vector<vector<int>>& adj) {
    queue<int> q; // 创建一个队列
    q.push(start); // 将起始顶点入队
    visited[start] = true; // 标记起始顶点为已访问

    while (!q.empty()) { // 当队列不为空时
        int v = q.front(); // 获取队首元素
        q.pop(); // 出队
        cout << v << " "; // 访问当前顶点

        for (int u : adj[v]) { // 遍历当前顶点的所有邻接顶点
            if (!visited[u]) { // 如果邻接顶点未被访问
                visited[u] = true; // 标记为已访问
                q.push(u); // 将邻接顶点入队
            }
        }
    }
}

三、图论经典问题

图论中有许多经典问题，以下是一些常见的图论问题及其简要介绍：

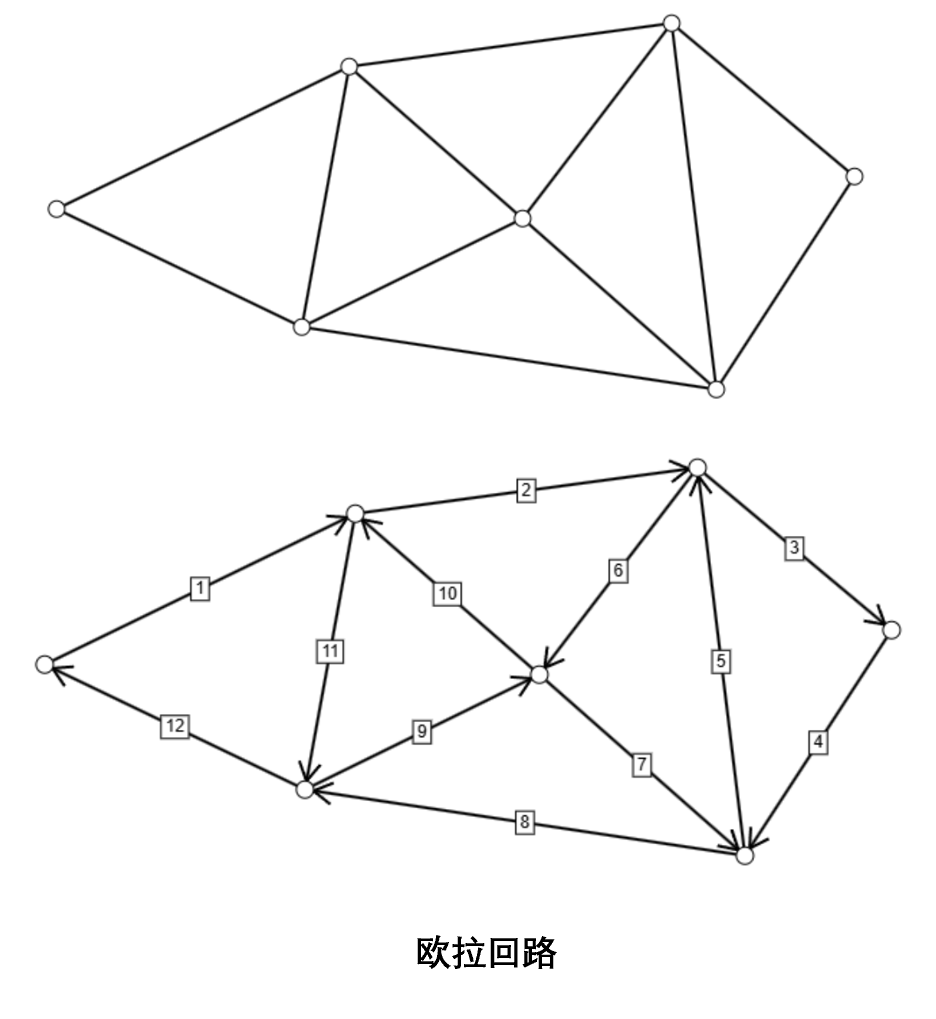
1. 欧拉路径与欧拉回路

欧拉路径是指经过图中每条边恰好一次的路径；欧拉回路是指经过图中每条边恰好一次的回路。带有欧拉回路的图称为欧拉图，而带有欧拉路径但不带有欧拉回路的图称为半欧拉图。

一个无向图存在欧拉回路的充要条件是所有顶点的度数都是偶数；存在欧拉路径的充要条件是至多有两个顶点的度数为奇数。一个有向图存在欧拉回路的充要条件是每个顶点的入度等于出度；存在欧拉路径的充要条件是至多有一个顶点的出度比入度多 1，至多有一个顶点的入度比出度多 1。

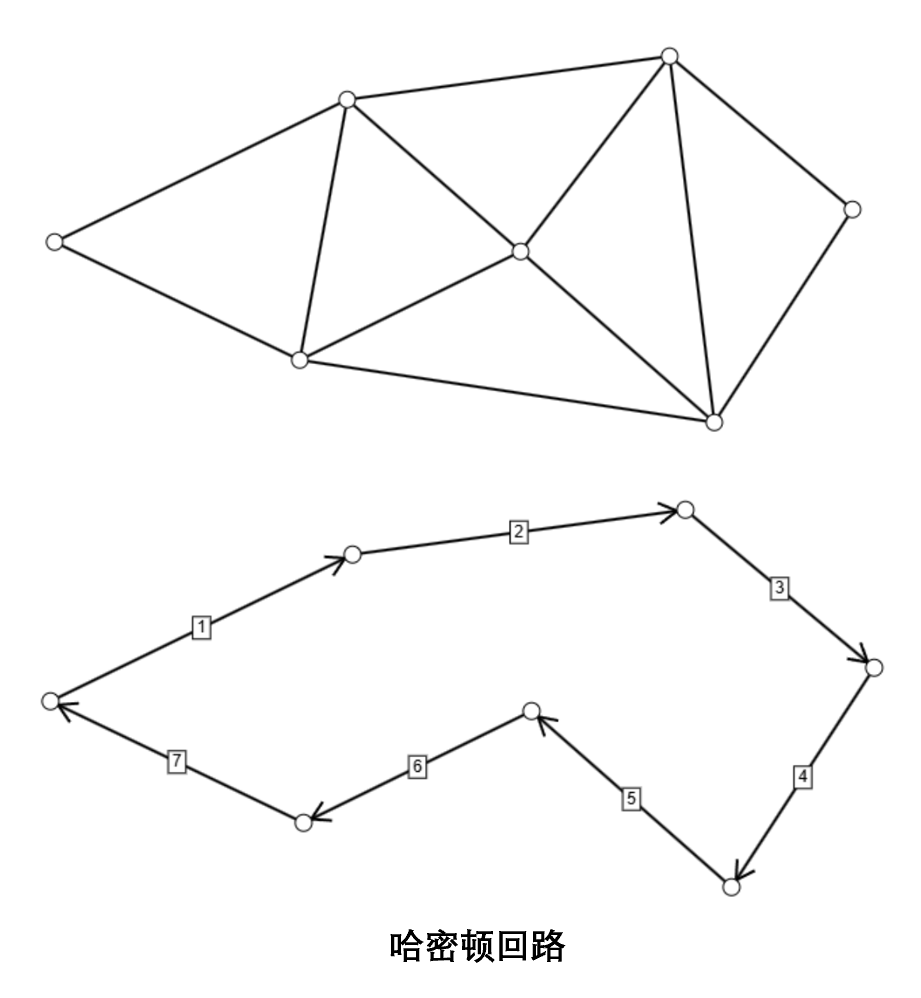
2. 哈密顿路径与哈密顿回路

哈密顿路径是指经过图中每个顶点恰好一次的路径；哈密顿回路是指经过图中每个顶点恰好一次的回路。带有哈密顿回路的图称为哈密顿图，而带有哈密顿路径但不带有哈密顿回路的图称为半哈密顿图。

一个图是否存在哈密顿路径或哈密顿回路是一个 NP 完全问题，没有已知的多项式时间算法可以解决，但是有一些充分或必要条件可以用于判定，此处就不介绍了。但一些特殊的图（如完全图）总是存在哈密顿回路。

3. 旅行商问题（TSP）

旅行商问题描述为：给定一组城市和它们之间的距离，如何选择一条道路使得商人每个城市走一遍后回到起点，且所走路径最短。用图论的语言表述就是：给定一个带权完全图，求一条哈密顿回路，使得路径长度最小。

这是一个经典的 NP 完全问题，通常使用近似算法求解。对于小规模的图，可以采用暴力搜索或分支定界法求得精确解。

4. 中国邮递员问题

中国邮递员问题也是一个 NP 完全问题，描述为：邮递员从邮局出发，走遍辖区内所有的街道至少一次（可以重复），最后回到邮局。要走怎样的路线全程才最短？用图论的语言表述就是：给定一个图，要求找到一个回路，使得每条边都被访问至少一次，并且路径长度最小。

显然，对于一个欧拉图，最优解就是欧拉回路；对于其他图，可以通过添加一些边使其变为欧拉图，然后求解欧拉回路。

5. 二分图匹配问题

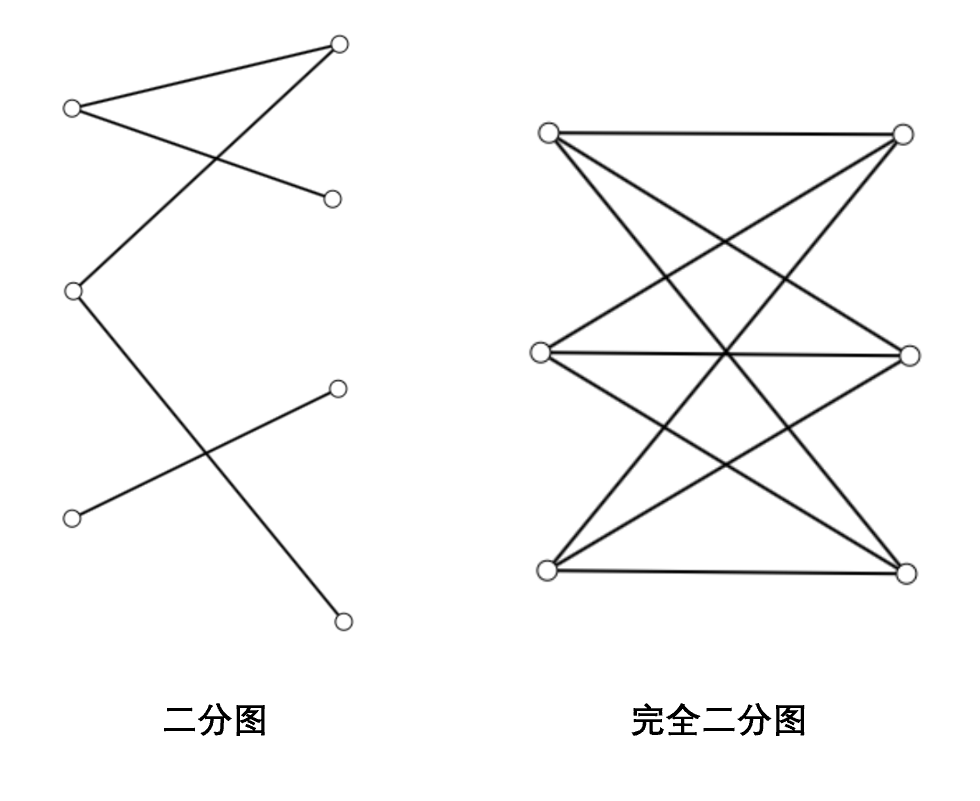
如果一个图的顶点集可以被分为两个不相交的子集，使得图中的每条边都连接这两个子集中的顶点，则称该图为二分图。一个图是二分图的充要条件是它不包含奇数长度的环（奇圈）。和完全图类似，我们可以定义完全二分图，即两个子集中的每个顶点都与另一个子集中的每个顶点相连。

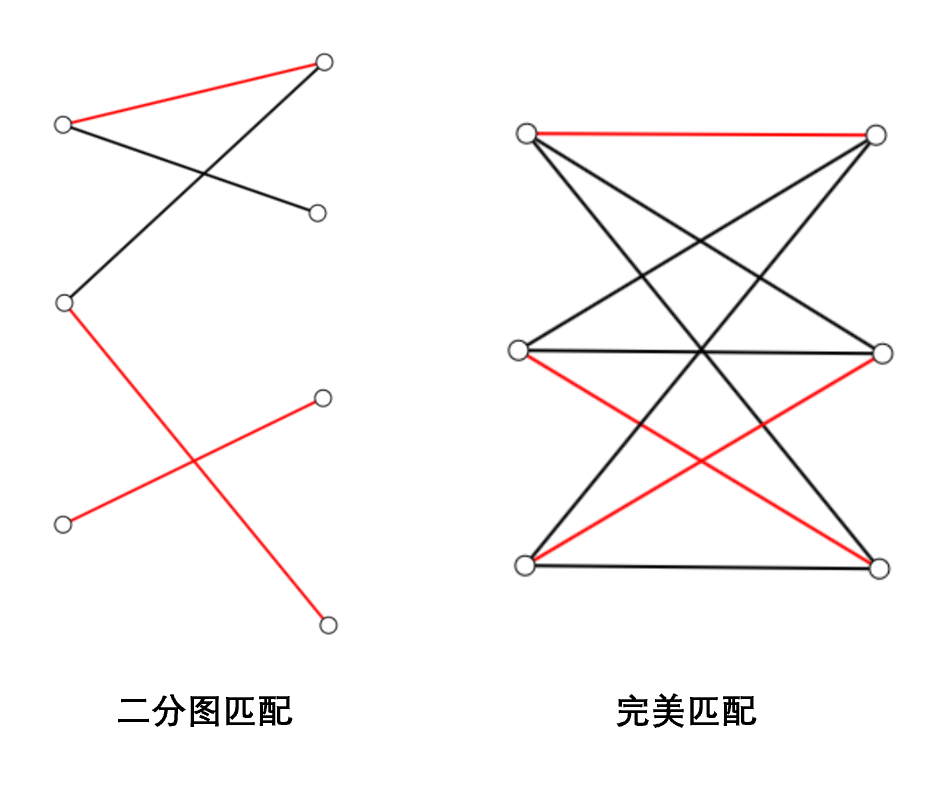
二分图匹配问题是指在一个二分图中，如何选择一些边，使得这些边所连的每个顶点至多被选中一次，并且所选边的数量最大。如果存在一个匹配，使得每个顶点都被选中，则称该匹配为完美匹配。一个二分图 $(V_1,V_2,E)$ 有完美匹配当且仅当 $|V_1|=|V_2|$ 且 $V_1$ 中任意 $k$ 个顶点至少与 $V_2$ 中的 $k$ 个顶点相连。

6. 图的平面性问题

图的平面性是指一个图是否可以在平面上绘制而不出现边的交叉。平面图有一些特殊的定义：由平面图的若干边所构成的一个“极小”区域（即区域内不含任何顶点或边）称为一个面。平面图有且仅有一个面积无穷的面，称为外部面，其他的面称为内部面。平面图的顶点、边和面的个数分别用 $V$、$E$ 和 $F$ 表示。平面图还有其对偶图：将平面图的每个面作为顶点，每条边作为连接两个面顶点的边。

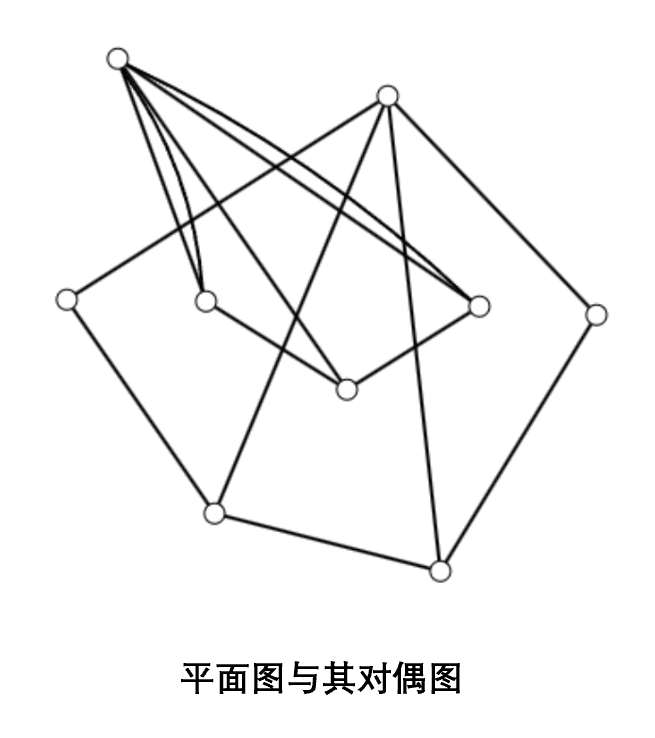
平面图有许多有趣的性质，如欧拉公式：$V - E + F = p(G)+1$，其中 $p(G)$ 是图的连通支个数。当图连通时，欧拉公式简化为 $V - E + F = 2$，可能有同学会注意到，这个公式与多面体的欧拉公式完全相同。事实上，平面图可以看作是多面体的一个投影。

图的平面性有表述较为简单的充要条件：一个图是可平面的当且仅当它不包含 $K_5$（五个顶点的完全图）或 $K_{3,3}$（两边各三个顶点的完全二分图）作为子图。但其判定算法仍然是 NP 完全的。

7. 图的着色问题

图的着色分为点着色、边着色和平面图的面着色。点着色是指给图的每个顶点分配一个颜色，使得相邻的顶点颜色不同；边着色是指给图的每条边分配一个颜色，使得相邻的边（即与同一个点相连）颜色不同；面着色是指给平面图的每个面分配一个颜色，使得相邻的面（即有公共边界）颜色不同。

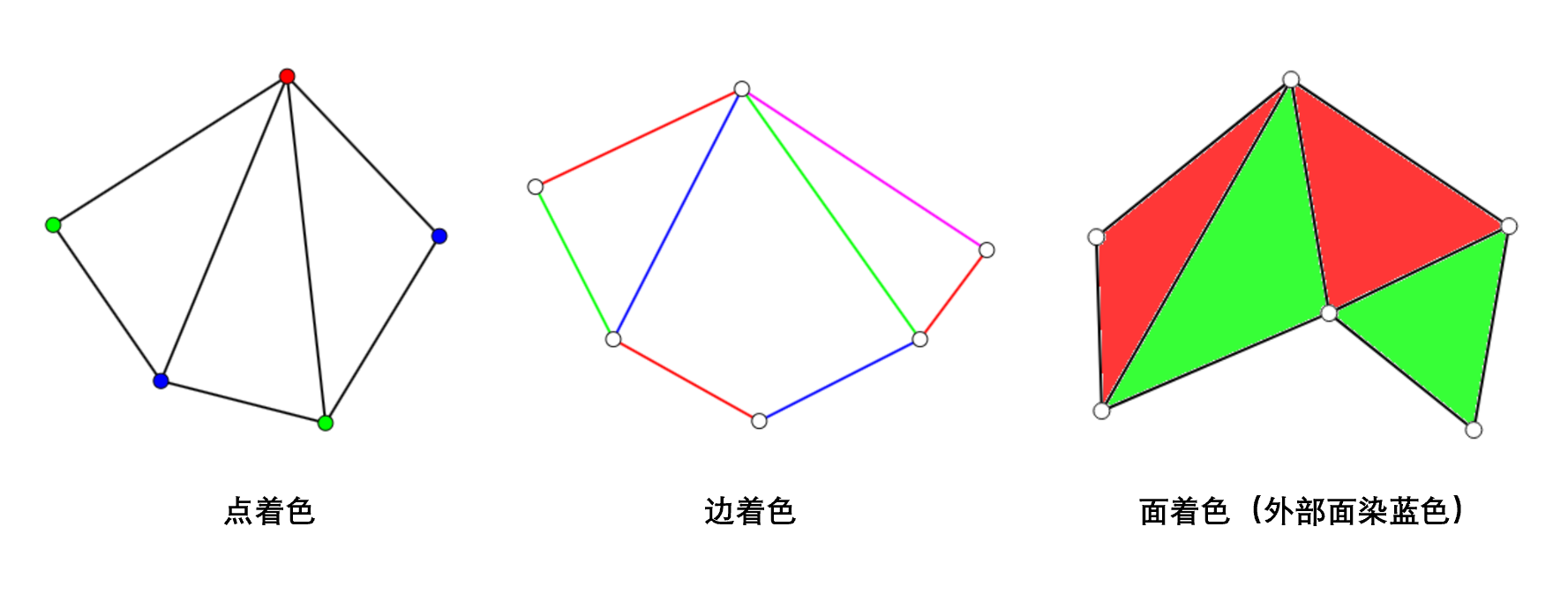
对于点着色问题，如果一个图既不是完全图也不是奇圈，则它的点色数（即最少需要多少种颜色才能使得相邻顶点颜色不同）不超过 $\Delta$，其中 $\Delta$ 是图中度数最大的顶点的度数。

对于边着色问题，我们可以在每条边上设置一个顶点；如果原图中两条边与同一个顶点相连，则在新图中将这两条边所对应的顶点连起来。这样，我们就将边着色问题转化为了点着色问题。此外，边着色也有自己的特殊结论：对一个简单图，其边色数只能是 $\Delta$ 或 $\Delta + 1$。但哪些图的边色数为 $\Delta$，哪些图的边色数为 $\Delta + 1$，至今仍是没有解决的问题。

对于平面图的面着色问题，则有著名的四色定理：任何平面图的面色数不超过 4。

四、图论算法简介

1. 最短路径

最短路径问题是图论中一个非常重要的问题，主要有三种常用的算法：Dijkstra 算法、Bellman-Ford 算法和 Floyd-Warshall 算法。

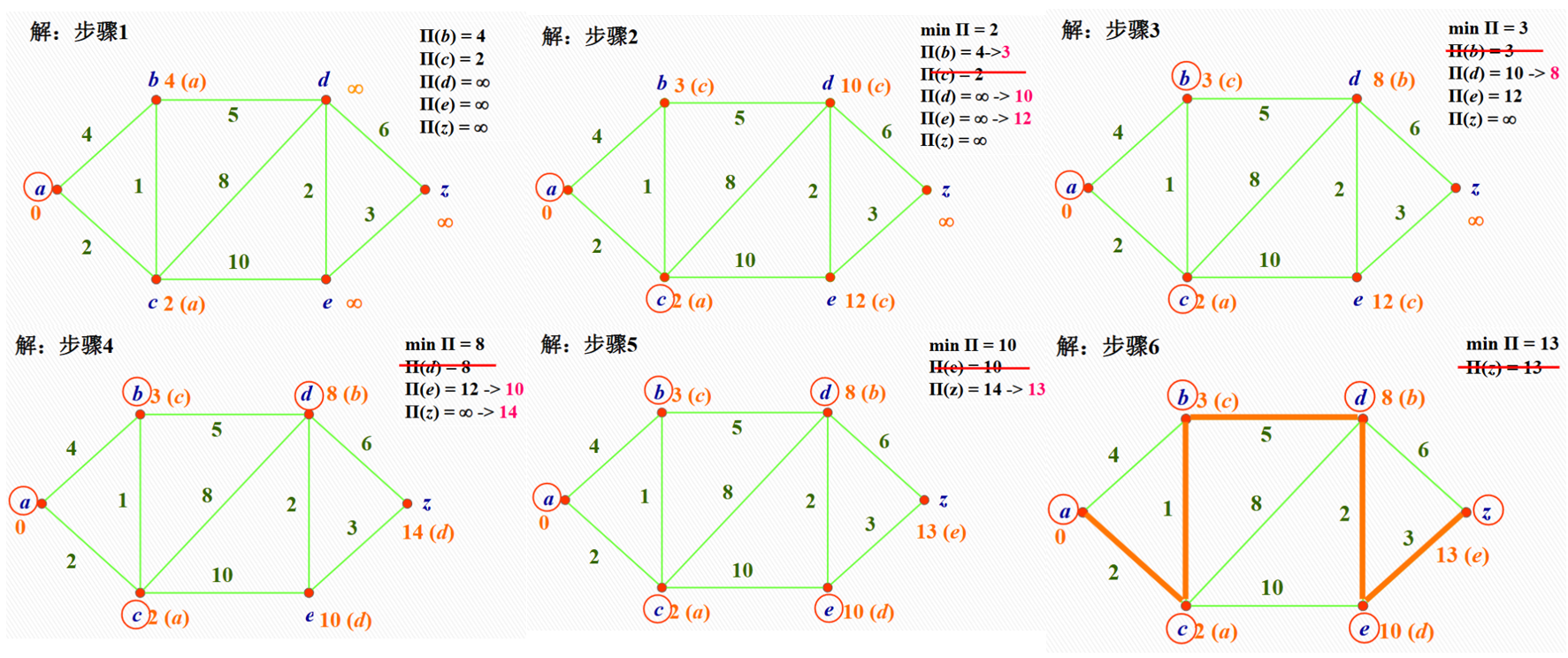
Dijkstra 算法用于求解单源最短路径问题。它的基本思路是按路径长度递增的次序产生最短路径。其正确性证明较为复杂，但计算步骤一看就懂。下面是一个例子：

下面是 Dijkstra 算法的伪代码：

void Dijkstra(int start, vector<vector<int>>& graph, vector<int>& dist) {
    int n = graph.size();
    vector<bool> visited(n, false); // 记录顶点是否已访问
    dist[start] = 0; // 起点到自身的距离为 0

    for (int i = 0; i < n - 1; ++i) { // 重复 n-1 次
        int u = -1; // 找到未访问的最小距离顶点
        for (int j = 0; j < n; ++j) {
            if (!visited[j] && (u == -1 || dist[j] < dist[u])) {
                u = j;
            }
        }
        visited[u] = true; // 标记顶点 u 为已访问

        for (int v = 0; v < n; ++v) { // 更新邻接顶点的距离
            if (graph[u][v] != INT_MAX && dist[u] + graph[u][v] < dist[v]) {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }
}

Dijkstra 算法的时间复杂度为 $O(V^2)$，其中 $V$ 是顶点数。如果使用优先队列优化，时间复杂度还能继续降低。但它只能处理非负权边的图（想想为什么？），在处理带有负权边的图时，我们需要使用 Bellman-Ford 算法。

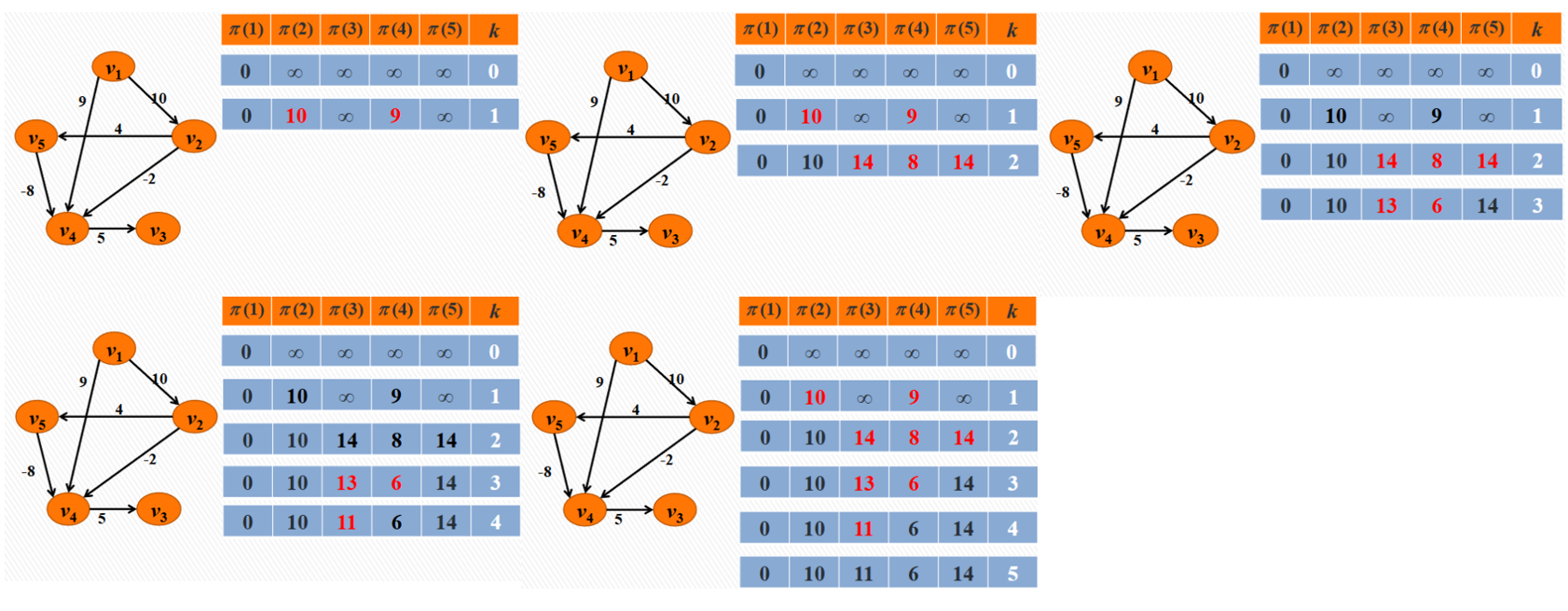
Bellman-Ford 算法的基本思路是根据路径长度从 $0$ 到 $|V|-1$，逐步迭代（更新后继节点）得到在当前路径长度范围内起点到各点的最短路，并最终得到起点到各点的最短路。下面是一个例子：

下面是 Bellman-Ford 算法的伪代码：

void BellmanFord(int start, vector<vector<int>>& graph, vector<int>& dist) {
    int n = graph.size();
    dist[start] = 0; // 起点到自身的距离为 0

    for (int i = 0; i < n - 1; ++i) { // 重复 n-1 次
        for (int u = 0; u < n; ++u) { // 遍历所有顶点
            for (int v = 0; v < n; ++v) { // 遍历所有边
                if (graph[u][v] != INT_MAX && dist[u] + graph[u][v] < dist[v]) {
                    dist[v] = dist[u] + graph[u][v]; // 松弛操作
                }
            }
        }
    }
}

Bellman-Ford 算法的时间复杂度为 $O(VE)$，其中 $E$ 是边数。可见 Bellman-Ford 算法的效率较低，尤其是在稠密图中，但它比 Dijkstra 算法更通用。

如果需要求解所有顶点对的最短路径问题，当然可以使用 Dijkstra 算法或 Bellman-Ford 算法对每个顶点进行一次，但我们有一个更简单的算法：Floyd-Warshall 算法。它的基本思路是逐步试着在原直接路径中增加中间节点，若加入中间点后路径变短，则修改之，直到所有节点试探完毕。它可以处理带有负权边的图。下面是 Floyd-Warshall 算法的伪代码：

void FloydWarshall(vector<vector<int>>& graph, vector<vector<int>>& dist) {
    int n = graph.size();
    dist = graph; // 初始化距离矩阵

    for (int k = 0; k < n; ++k) { // 遍历所有中间节点
        for (int i = 0; i < n; ++i) { // 遍历所有起点
            for (int j = 0; j < n; ++j) { // 遍历所有终点
                if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX &&
                    dist[i][j] > dist[i][k] + dist[k][j]) {
                    dist[i][j] = dist[i][k] + dist[k][j]; // 松弛操作
                }
            }
        }
    }
}

Floyd-Warshall 算法的时间复杂度为 $O(V^3)$，其中 $V$ 是顶点数。对于非负边权图，其效率与运行 $V$ 次 Dijkstra 算法相当，但其代码实现更简单；对于带有负边权的图，其效率高于运行 $V$ 次 Bellman-Ford 算法。

2. 拓扑排序

拓扑排序是指对一个有向无环图进行排序，使得对于每一条边 $(u, v)$，顶点 $u$ 在排序中出现在顶点 $v$ 之前。拓扑排序的基本思路是：首先找到一个入度为 0 的顶点，将其加入排序结果中；然后将该顶点从图中删除，并更新其他顶点的入度；重复上述过程，直到所有顶点都被处理。下面是一个基于栈的拓扑排序的伪代码：

void TopologicalSort(vector<vector<int>>& graph, vector<int>& result) {
    int n = graph.size();
    vector<int> inDegree(n, 0); // 记录每个顶点的入度
    // 计算每个顶点的入度
    for (int u = 0; u < n; ++u) {
        for (int v : graph[u]) {
            inDegree[v]++;
        }
    }
    stack<int> s; // 使用栈来存储入度为 0 的顶点
    for (int i = 0; i < n; ++i) {
        if (inDegree[i] == 0) {
            s.push(i);
        }
    }
    while (!s.empty()) {
        int u = s.top(); // 获取栈顶元素
        s.pop();
        result.push_back(u); // 将顶点加入结果

        for (int v : graph[u]) { // 遍历所有邻接顶点
            inDegree[v]--; // 更新入度
            if (inDegree[v] == 0) {
                s.push(v); // 如果入度为 0，则将其加入栈中
            }
        }
    }
}

拓扑排序的一个重要应用是关键路径问题。关键路径问题是指：对于一个由若干个任务组成的项目，每个任务有各自的耗时，且任务之间可能存在依赖关系（即某些任务必须在其他任务完成后才能开始），如何安排这些任务的开始时间，使得整个项目的完成时间最短。如果将其建模为一个有向无环图，则整个项目的最短完成时间就是图中最长的路径长度。将图进行拓扑排序后，我们可以从起点开始，依次计算每个顶点的最早开始时间，从而得到整个项目的最短完成时间。下面是一个例子，图中 $N$ 是虚拟节点，表示项目的终点。

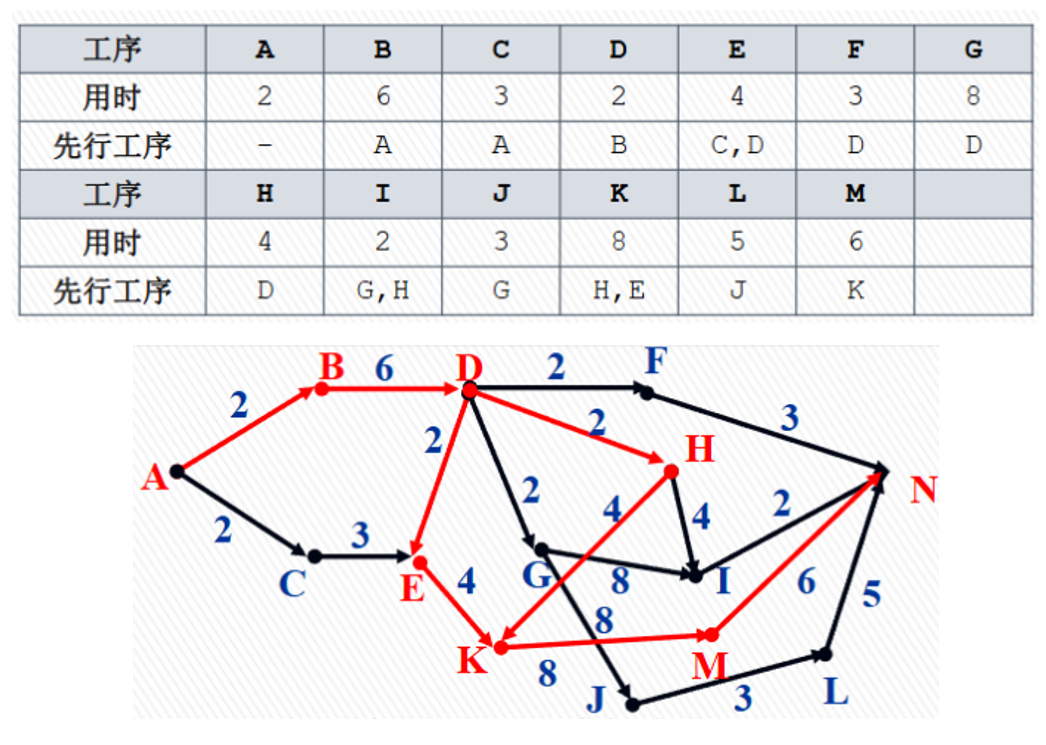
五、图的应用

我们来看一个有趣的问题：

集合 $A=\{1,2,3,4,5,6,7,8\}$，定义 $M=\{(x,y)|x\in A,y\in A\}$。从 $M$ 中选出一些点排成一列：$(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)$。如果对于任意相邻两个点 $(x_i,y_i),(x_{i+1},y_{i+1})$ 满足以下等式 $\begin{cases} |x_{i+1}-x_i|=3\\|y_{i+1}-y_i|=4 \end{cases}$ 或 $\begin{cases} |x_{i+1}-x_i|=4\\|y_{i+1}-y_i|=3 \end{cases}$，那么就称该序列为一条 $k$ 列。证明：$M$ 中所有元素的任意排列都不构成 $k$ 列。

如果我们把 $M$ 看成一个 $8\times 8$ 的棋盘，那么题目条件其实是在说，如果有一匹马可以按 $3\times 4$ 的方式跳，那么不存在一条路径，使得马可以从一个点出发，经过棋盘上的每个格子恰好一次。这其实就是前面所说的哈密顿路径问题。

实际上，这是今年高考数学北京卷的压轴大题！可见，图论的实际应用非常广泛。不仅如此，图论还可以用来解决很多实际问题，如网络流、社交网络分析、地图导航等。

希望同学们通过本期的内容，能够对图论有一个初步的了解，为后续学习《数据结构》打下基础。下期我们将介绍树论相关的知识，希望大家继续关注肆叁小灶，期待下期内容的发布！