肆叁小灶第一讲 Standard Template Library (STL)

肆叁小灶第一讲，介绍了 STL 库的基本用法，主要包括 deque 和 set 的使用方法以及一些常用的 STL 函数。

笃实43班的同学们大家好，这里是学委小组的第一期推送。

经过半学期的沉淀（摸鱼），在小组内部以及和吴导商量过后，我们已经有了接下来工作计划的雏形：由褚一枫同学来负责制作介绍编程相关知识的推送，而邓写意同学负责编程月赛等活动的组织工作。

考虑到篇幅所限，每期介绍的内容不会很多、很深，会以一些课上不讲的小技巧以及一些实用软件的简略介绍为主，更多细节最终还是要靠大家自己去探索。

本学期内我们预计将发布四期：

1. STL
2. Markdown 与 LaTeX
3. 常用数学软件
4. 常用编程 AI

废话不多说，让我们直接进入正题。

一、What is STL ?

如果直接去百度上搜索，大概率会得到如下结果：

STL 是 C++ 标准模板库（Standard Template Library）的缩写，是 C++ 标准库的重要组成部分，不仅是一个可复用的组件库，而且是一个包罗数据结构与算法的软件框架。

问题来了，数据结构又是什么？

简而言之，数据结构就是数据存储在计算机里的样子。比如一维数组就是一个最简单的数据结构，数据在内存里连续排列，可以按照顺序逐个访问。

更“高级”一点的数据结构还包括二维数组（矩阵）、链表、栈、队列、树、图等等，其中二维数组和链表我们已经在程设课上接触过了，而栈和队列分别是深度优先搜索（DFS）和广度优先搜索（BFS）的底层架构，再过两周程设课就会讲到，至于树和图，则是离散数学和数据结构这两门课的常客。

就像我们只需要引入标准输入输出库 stdio.h 就可以直接实现输入和输出而无需进行命令行操作一样，我们只需要引入 STL 库和 std 命名空间，就可以通过一些简单的函数直接实现这些数据结构。

而不同于标准输入输出库，STL 库是很多个库的合称，如 vector、stack、algorithm 等，考虑到篇幅所限，我们今天主要介绍两个模板：双端队列 deque 和集合 set。

二、What is Deque ?

还记得前面说到的栈和队列吗？我们先简要介绍一下这两个数据结构。

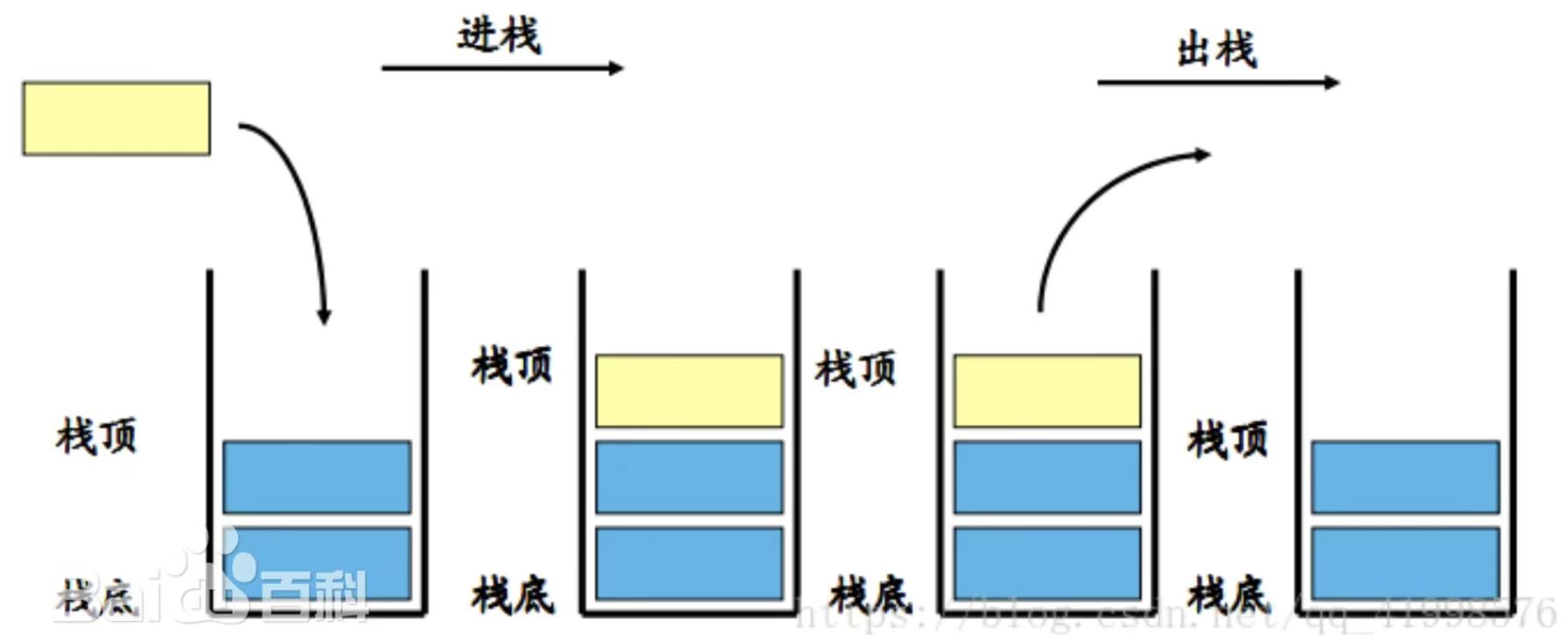
栈的特点是“先进后出”，简而言之，可以把它理解成往一个桶里一边塞衣服一边把衣服取出来，显然只能取出叠在最上面的衣服，而塞的越早的衣服就叠在越下面，也就要越晚才能再次被取出来。

举一个简单的例子，按顺序进行以下操作：

1 入栈，2 入栈，3 入栈，3 出栈，2 出栈，4 入栈，4 出栈，1 出栈，5 入栈，5 出栈。

这样我们就成功的把 [1,2,3,4,5] 通过一个栈转化成了 [3,2,4,1,5]。

下面这张图可以辅助大家理解：

而队列则和栈恰好相反，特点是“先进先出”，可以理解为在食堂排队，先入队的自然能先领到午饭。

同样举一个简单的例子：

1 入队，2 入队，3 入队，1 出队，4 入队，2 出队，3 出队，5 入队，4 出队，5 出队。

可能你会发现，这样一通操作下来不还是 [1,2,3,4,5] 吗？没错，因为这并不是队列的正确用途。等大家学到广度优先搜索就会明白队列的作用了。

同样给一张图辅助大家理解：

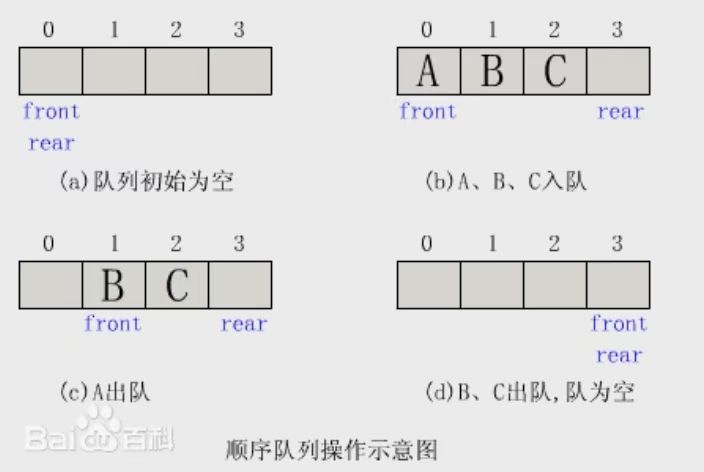
所以讲了那么久的栈和队列，Deque呢？

我知道你很急，但你先别急。

Deque 的全称是 Double Queue（双端队列），简而言之，它既可以从前面插入可以从后面插入，既可以从前面取出也可以从后面取出。

可见，数组、栈和队列都可以视作 Deque 的一个“特殊情况”：数组只从后面插入而不取出，栈从后插入、从后取出，队列从后插入、从前取出。那么二维数组呢？也很简单，只需要让一个 Deque 的每个元素又都各是一个 Deque 即可。而且 Deque 模板无需提前给定大小，也就是自动实现了动态数组的功能。

以下是参考代码：

#include<stdio.h>
#include<deque>
#include<tuple>
#include<algorithm>
using namespace std;
bool tuple_cmp(tuple<int,int> a,tuple<int,int> b){
    if(get<0>(a)==get<0>(b)) return get<1>(a)>get<1>(b);
    return get<0>(a)>get<0>(b);
}//基于tuple的二元组降序排序函数
void create_matrix(){
    deque<deque<int>> matrix;
    int n,m;
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++){
        deque<int> temp;
        for(int j=0;j<m;j++){
            int x;
            scanf("%d",&x);
            temp.push_back(x);
        }
        matrix.push_back(temp);
    }//输入：先创建临时一维deque存储一行，再把一整行导入二维deque
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            printf("%d ",matrix[i][j]);
        }
        printf("\n");
    }//输出：deque允许通过下标访问
}//基于deque的动态二元数组
void create_sorted_tuple(){
    deque<tuple<int,int>> sorted_tuple;
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        int x,y;
        scanf("%d %d",&x,&y);
        tuple<int,int> temp=make_tuple(x,y);
        sorted_tuple.push_back(temp);
    }//输入：先创建临时tuple存储二元组，再将整个tuple导入deque
    stable_sort(sorted_tuple.begin(),sorted_tuple.end(),tuple_cmp);//对tuple组成的deque进行降序排序
    for(int i=0;i<n;i++){
        printf("%d %d\n",get<0>(sorted_tuple[i]),get<1>(sorted_tuple[i]));
    }//输出：tuple不允许用下标[0][1]访问，只能用get函数
}//基于deque&tuple&sort的降序二元组数组
void create_stack(){
    deque<int> stack;
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        int x;
        scanf("%d",&x);
        stack.push_back(x);
    }//入栈
    for(int i=0;i<n;i++){
        printf("%d ",stack.back());
        stack.pop_back();
    }//出栈
}//基于deque的栈
void create_queue(){
    deque<int> queue;
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        int x;
        scanf("%d",&x);
        queue.push_back(x);
    }//入队
    for(int i=0;i<n;i++){
        printf("%d ",queue.front());
        queue.pop_front();
    }//出队
}//基于deque的队列
int main(){
    int op;
    scanf("%d",&op);
    switch(op){
        case 1: 
          create_matrix();
          break;
        case 2: 
          create_sorted_tuple();
          break;
        case 3: 
          create_stack();
          break;
        case 4: 
          create_queue();
          break;
    }
    return 0;
}

上面的代码中，case 1&3&4 已经包括了如何创建一个 Deque、如何从前后插入和取出元素，接下来我们解释一下 case 2 中用到的多元组 tuple 和 sort 函数。

简而言之，tuple 是几个子元素组成的有序对，可以看成结构体的平替。case 2 的代码中已经包括了如何创建一个 tuple 元素、如何取出一个 tuple 中特定位置的子元素。

sort 函数位于 algorithm 库中，时间复杂度（可以简单理解为算法的效率）为 O(nlgn)，远远优秀于程设课讲的 O(n²) 的冒泡排序。其默认参数为对单元素（即非 tuple、pair、struct）组成的一维数组进行升序排列，因此上面 case 2 在对 tuple 进行降序排列时，需要自己写一个比较函数。此外，case 2 中使用了 stable_sort，其与 sort 的区别在于 stable_sort 会保持排序前后两个相同元素的相对位置，而 sort 不一定。

再补充一点，实际上 deque 库中同样有在任意位置插入或删除的函数 d.insert(n,x) 和 d.erase(n)，但由于底层架构的原因这两个操作的复杂度都是 O(n) 而非 O(1)，无法平替链表。如需使用 STL 实现链表可以引入 list 库，这里由于篇幅所限就不展开了。留给读者作为课后习题

三、What is Set ?

高中数学告诉我们，集合具有互异性，而 STL 中的 set 也是如此，可以将输入的数据自动去重。不同的是，它还能实现自动排序。如向一个 set 中输入 [1,5,3,5,7,4]，输出的结果会是 [1,3,4,5,7]。值得一提的是，set 的插入操作时间复杂度为 O(lgn)，也就是说它可以做到以 sort 函数的效率持续维护一个升序数组。

此外，STL 也提供了 multiset（升序，不去重）、unordered_set（无序，去重）、unordered_multiset（无序，不去重）等功能，可以按需使用。

以下是参考代码：

#include<stdio.h>
#include<set>
#include<algorithm>
using namespace std;
int main(){
    set<int> s1,s2,cap,cup,diff;
    int n1,n2;
    scanf("%d", &n1);
    for(int i=0; i<n1; i++){
        int x;
        scanf("%d", &x);
        s1.insert(x);
    }//输入s1
    for(set<int>::iterator it=s1.begin(); it!=s1.end(); it++){
        printf("%d ", *it);
    }//输出s1：set不允许通过下标访问，只能通过迭代器访问
    printf("\n");
    scanf("%d", &n2);
    for(int i=0; i<n2; i++){
        int x;
        scanf("%d", &x);
        s2.insert(x);
    }//输入s2
    for(set<int>::iterator it=s2.begin(); it!=s2.end(); it++){
        printf("%d ", *it);
    }//输出s2
    printf("\n");
    set_union(s1.begin(), s1.end(), s2.begin(), s2.end(), inserter(cup, cup.begin()));//计算s1∪s2
    for(set<int>::iterator it=cup.begin(); it!=cup.end(); it++){
        printf("%d ", *it);
    }//输出s1∪s2
    printf("\n");
    set_intersection(s1.begin(), s1.end(), s2.begin(), s2.end(), inserter(cap, cap.begin()));//计算s1∩s2
    for(set<int>::iterator it=cap.begin(); it!=cap.end(); it++){
        printf("%d ", *it);
    }//输出s1∩s2
    printf("\n");
    set_difference(s1.begin(), s1.end(), s2.begin(), s2.end(), inserter(diff, diff.begin()));//计算s1-s2
    for(set<int>::iterator it=diff.begin(); it!=diff.end(); it++){
        printf("%d ", *it);
    }//输出s1-s2
    printf("\n");
    set<int>::iterator it=cup.find(3);//寻找并集中的第一个3
    set<int>::iterator a=cup.lower_bound(3);//寻找并集中第一个≥3的数
    set<int>::iterator b=cup.upper_bound(3);//寻找并集中第一个＞3的数
    printf("%d %d\n", *it, distance(cup.begin(),it));//输出第一个3的“下标”
    printf("%d %d\n", distance(cup.begin(),a), *a);//输出第一个≥3的数的“下标”
    printf("%d %d\n", distance(cup.begin(),b), *b);//输出第一个>3的数的“下标”
    return 0;
}

上面的代码中已经包含了如何创建一个 set、如何向 set 中插入元素，接下来我们解释一下代码中用到的迭代器 iterator 和几个 algorithm 库函数。

强调一点：set 与 deque 不同，不能直接通过下标访问，只能通过地址访问。而 iterator 可以简单理解为 STL 容器专用指针，注意这里不能直接用指针的原因是通过 STL 容器存储的元素在内存中的位置不一定是连续的，用指针的 ++ 操作很可能访问到内存中错误的位置，而使用 iterator 就可以避免这个问题。

此外，代码中用到了七个 algorithm 库函数，我们分别做一下简要介绍：

1. set_union：求两个有序列表的并集
2. set_intersection：求两个有序列表的交集
3. set_difference：求两个有序列表的差集
4. s.find(x)：返回列表中x元素第一次出现的地址
5. s.lowerbound(x)：返回有序列表中第一个≥x的元素的地址
6. s.upperbound(x)：返回有序列表中第一个>x的元素的地址
7. distance：求两个迭代器之间的距离

上面的代码稍作修改就可以无痛速通这道程设 OJ 作业：

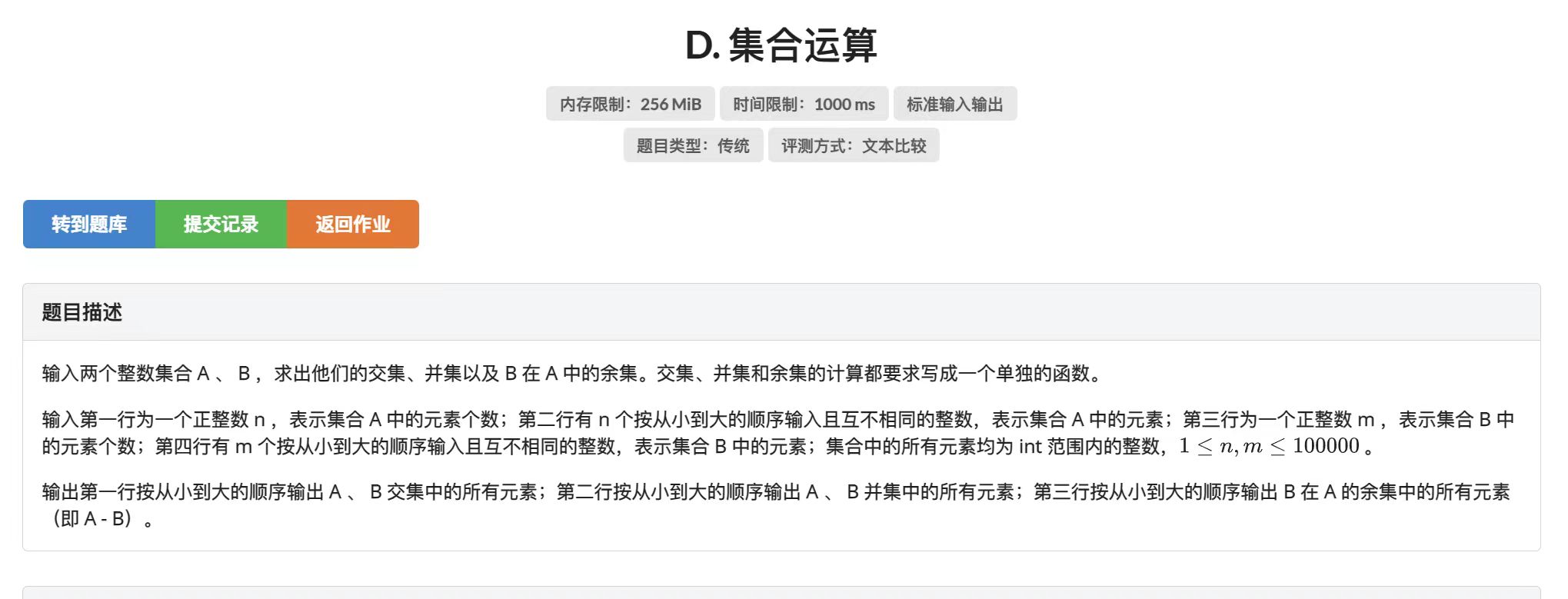
当然，这道题的输入数据已经是升序排列的了，也就不需要再使用 set 容器，直接使用普通数组或前面介绍的 deque 容器配合上述 algorithm 库函数即可。实际上 algorithm 库中还有很多有奇效的函数，如 next_permutation 等等，由于篇幅所限就不展开了。同样留作课后习题

后记

考虑到初学 C 语言的同学了解底层架构的必要性，STL 库在 OJ 作业和期末考试中是禁用的，切勿模板一时爽期末火葬场（据学长所说数据结构课也是禁用 STL 的）。然而在大作业中 STL 库可以随意使用，能够大幅提升代码构建效率和运行效率。此外，对于想参加算法竞赛的同学，个人建议在熟练使用的同时也去了解一下 STL 库函数的底层实现，可以大大加深对数据结构与算法优化的理解。

这期的内容到这里就结束了，感谢大家读到这里。下期我们将为大家简要介绍 Markdown 和 LaTeX 环境的配置过程和入门语法，这些内容对正在修读离散数学（1）的同学可能并不陌生，希望能够帮到未选课的同学。